Find the angle between the two tangents from the origin to the circle ${(x - 7)}^{2} + {(y + 1)}^{2} = 25$

Text Solution

Verified by Experts

The correct Answer is: $90^{\circ}$

Centre of the circle is C(7,-1) and radius , $C M = 5$ .

$O C = \sqrt{7^{2} + {(- 1)}^{2}} = 5 \sqrt{2}$
$∴ \sin θ = \frac{C M}{O C} = \frac{5}{5 \sqrt{2}} = \frac{1}{\sqrt{2}}$
$\Rightarrow θ = 45^{\circ}$
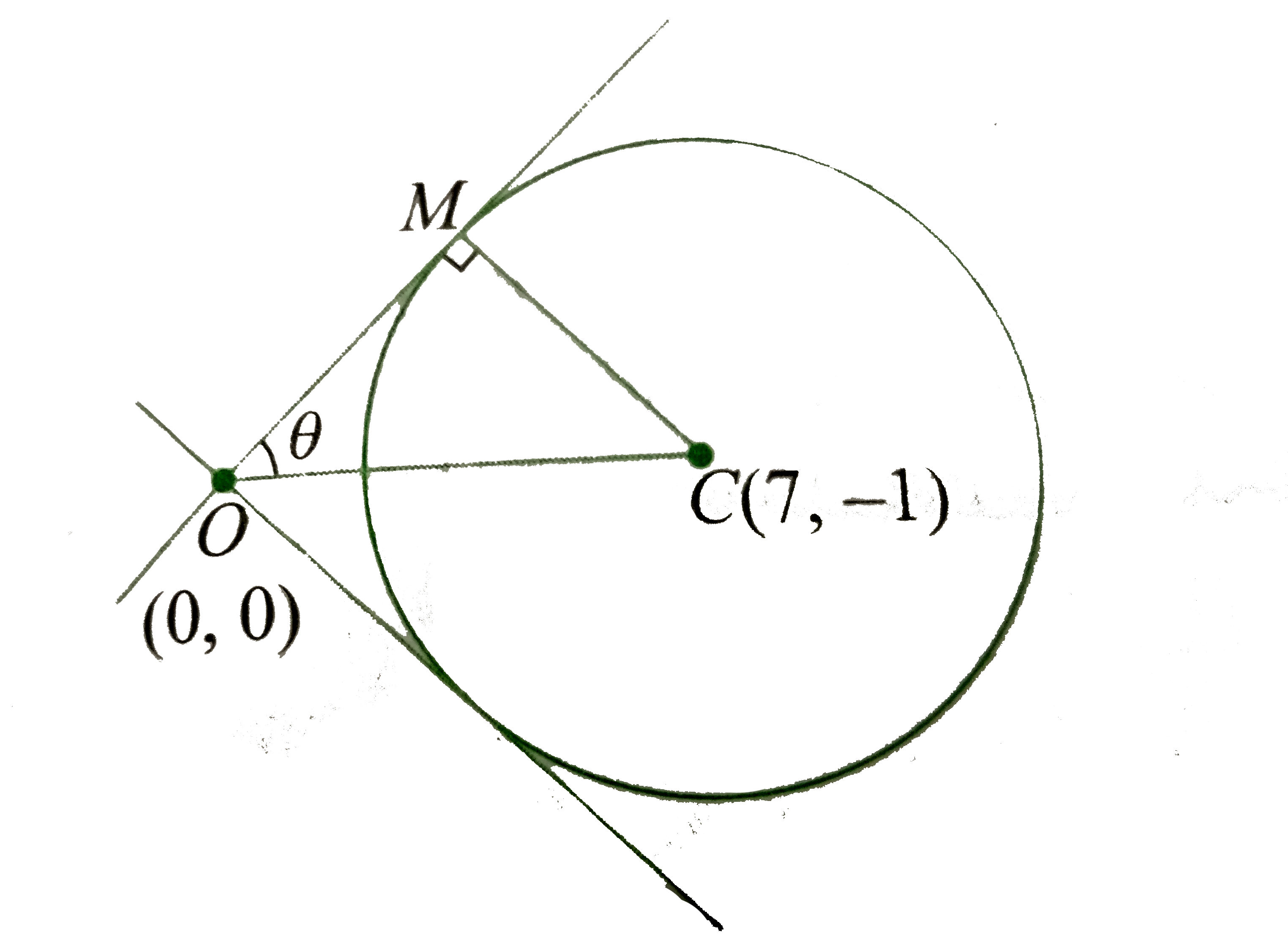
Hence, angle between tangents is $90^{\circ}$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Find the angle between the two tangents from the origin to the circle ${(x - 7)}^{2} + {(y + 1)}^{2} = 25$
A $π / 3$
B $π / 6$
C $π / 2$
D0
Question 2 - Select One
Find the angle between the two tangents from the origin to the circle ${(x - 7)}^{2} + {(y + 1)}^{2} = 25$
A $π / 3$
B $π / 6$
C $π / 2$
D0
Question 3 - Select One
Find the angle between the two tangents from the origin to the circle ${(x - 7)}^{2} + {(y + 1)}^{2} = 25$
A $\frac{π}{3}$
B $\frac{π}{6}$
C $\frac{π}{2}$
D $\frac{π}{8}$

CENGAGE PUBLICATION-CIRCLE -CONCEPT APPLICATION EXERCISE 4.3

Home
Ask Doubt
Profile