Find the are of the region bounded by the curve $y = x^{2} + 2$ and the lines $y = x, x = 0 and 3$

Video Solution

Text Solution

Verified by Experts

$y = x^{2} + 2 \Rightarrow x^{2} = (y - 2)$
Clearly , $x^{2} = (y - 2)$ represents an upward parabola with its vertex at A (0,2)

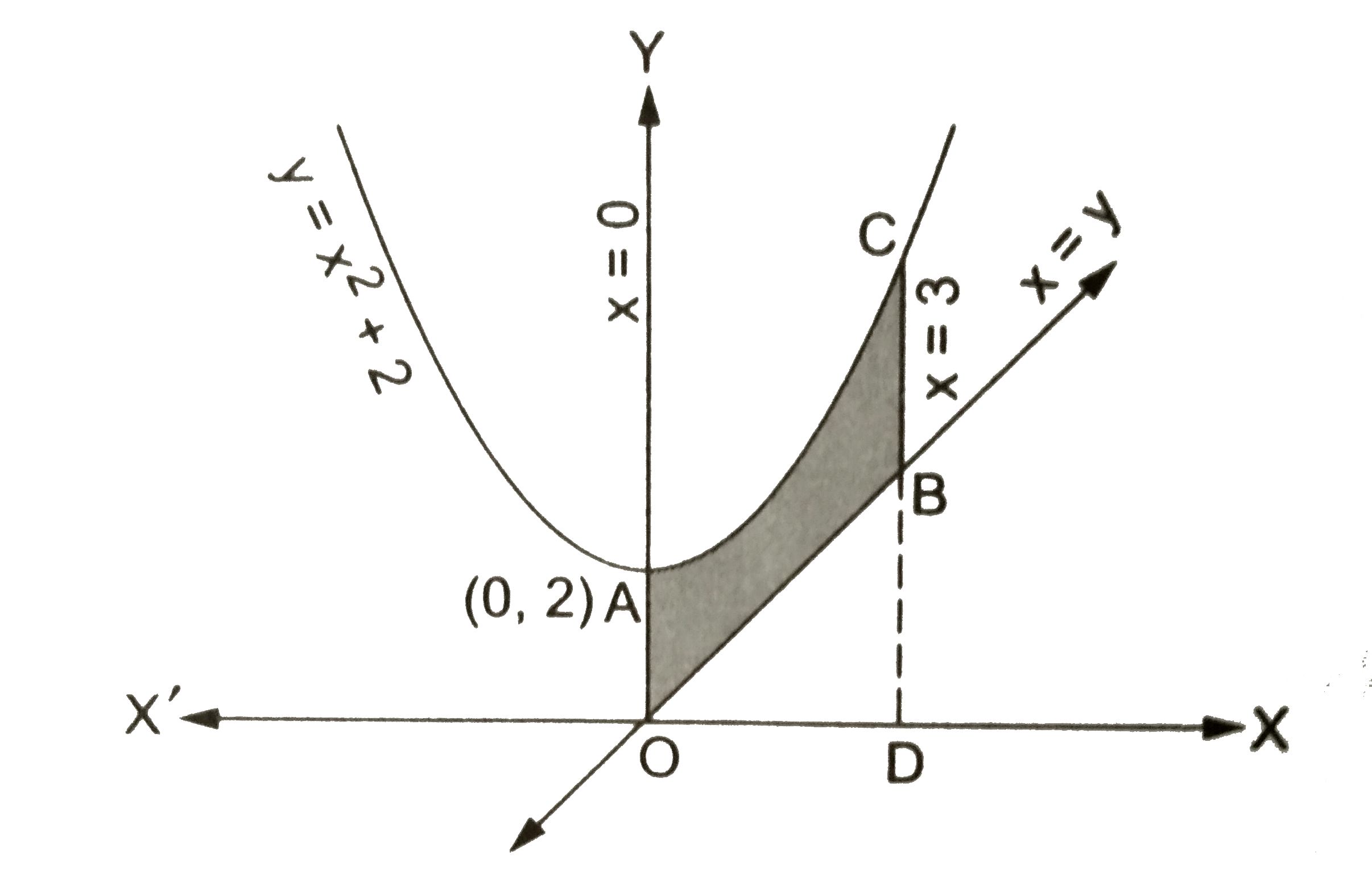
Also , y = x represents the straight line , making an angle of $45^{\circ}$ with the positive direction of the x-axis .
And x = 0 is the y-axis , while x = 3 represents a ling parallel to the y-axis at a distance of 3 units from it .
Thus , the shaded region in the given figure is the required area .
$∴$ required area = (area ODCAO) - (area ODBO)
$= 3 \int 0 (x^{2} + 2) d x - 3 \int 0 x d x$
= ${[\frac{x^{3}}{3} + 2 x]}_{0}^{3} - {[\frac{x^{2}}{2}]}_{0}^{3} = (15 - \frac{9}{2}) = \frac{21}{2}$ sq units .
Hence , the required area is $\frac{21}{2}$ sq units .

Updated on:21/07/2023