Question

Find the area bounded by the curve ${\displaystyle x^2=4y}$
and the straight line ${\displaystyle x=4y-2.}$

Options

A. `(9)/(8)` sq units
B. `(3)/(8)` sq unit
C. `(1)/(8)` sq unit
D. None of these

Answer

A

Explanation

Given curves are `x^(2)=4y" ... (i)"`
and `x = 4y - 2 " … (ii)"`
For intersection point, put the value of 4y from Eq. (i) in Eq. (ii), we get `x^(2)=x+2`
`implies x^(2)-x-2=0`
`implies (x-2)(x+1)=0`
implies x=2,-1
When x = 2, then from Eq. (ii), we get
4y = 2 + 2 implies y = 1
When x = - 1, then from Eq. (ii) we get
4y = 2 - 1 = 1
`implies y = (1)/(4)`
`therefore` The line meets the parabola at the points `B(-1,(1)/(4))` and A(2, 1).

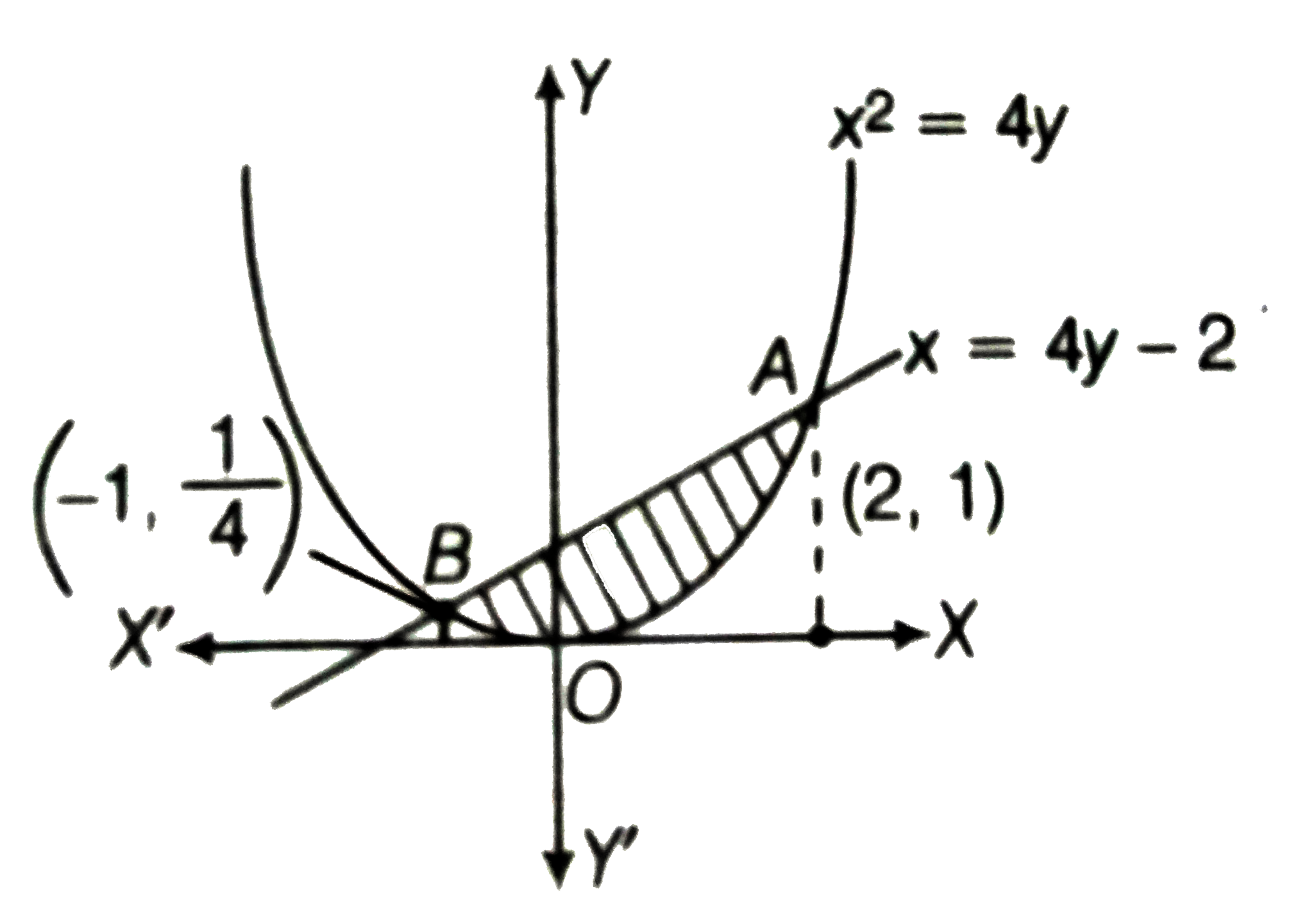
Required area = (Area under the line x = 4y - 2)-(Area under the parabola `x^(2)=4y`)
`=int_(-1)^(2)((x+2)/(4))dx-int_(-1)^(2)(x^(2))/(4)dx`
`=(1)/(4){[(x^(2))/(2)+2x]_(-1)^(2)-(1)/(4)[(x^(3))/(3)]_(-1)^(2)`
`=(1)/(4){(2^(2))/(2)+2xx2-((1)/(2)-2)}-(1)/(12)[2^(3)-(-1)^(3)]`
`=(1)/(4)(6+(3)/(2))-(1)/(12)xx9=(15)/(8)-(3)/(4)=(9)/(8)` sq units
Therefore, required area is `(9)/(8)` sq units.