Find the area bounded by the line y=x, the x-axis and the ordinates x=−1 and x=2
Video Solution
Text Solution
We know that y=x Is the line passing through the origin and making an angle of 45∘ with the x-axis as shown in the given figure
Now we have to find the area of the shaded region
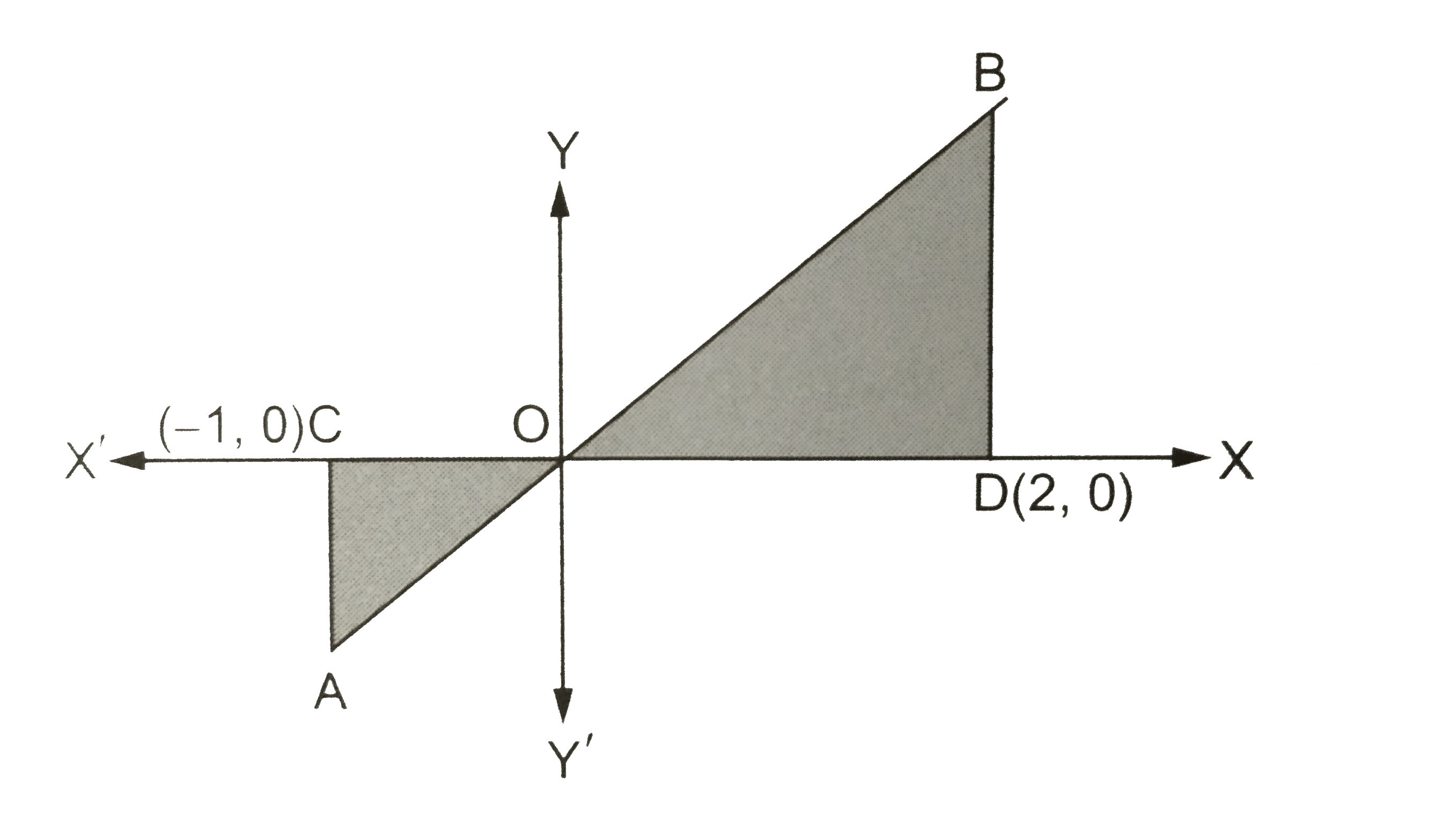
Required area
=(area ODBO )+ (area OACO)
=2∫0dx+0∫−1(−y)dx [∵area OACO is below the x-axis ]
=2∫0dx+0∫−1(−x)dx
=[x22]20+[−x22]0−1=[2+12]=52 sq units
Hence , the required area is 52 sq units
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
Area bounded by the line 2x+y=4, the X-axis and the ordinate at x=−2 is
A12B15C16DNone of these
Find the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=1andx=1.
View SolutionUsing integration, find the area of the region bounded by the line y−1=x,thex−a xi s and the ordinates x=−2andx=3.
View SolutionUsing integration, find the area of the region bounded by the line y-1 = x, the x-axis, and the ordinates x = -2 and x = 3.
View SolutionFind the area bounded by y=x−1, the x-axis and the ordinates x=1,x=3.
View SolutionThe area bounded by the line y=mx+c, X -axis and the ordinates x=a, x=b, is
View SolutionFind the area bounded by the curve y=cosx, x-axis and the ordinates x=0 and x=2π.
View SolutionFind the area bounded by the curve y=logx, x-axis and the ordinates x=1&x=e.
View Solution
