Find the area enclosed between the parabola $y^{2} = 4 a x$ and the line $y = m x$ .

Video Solution

Text Solution

Verified by Experts

The given equation are
$y^{2} = 4 a x \dots (i)$
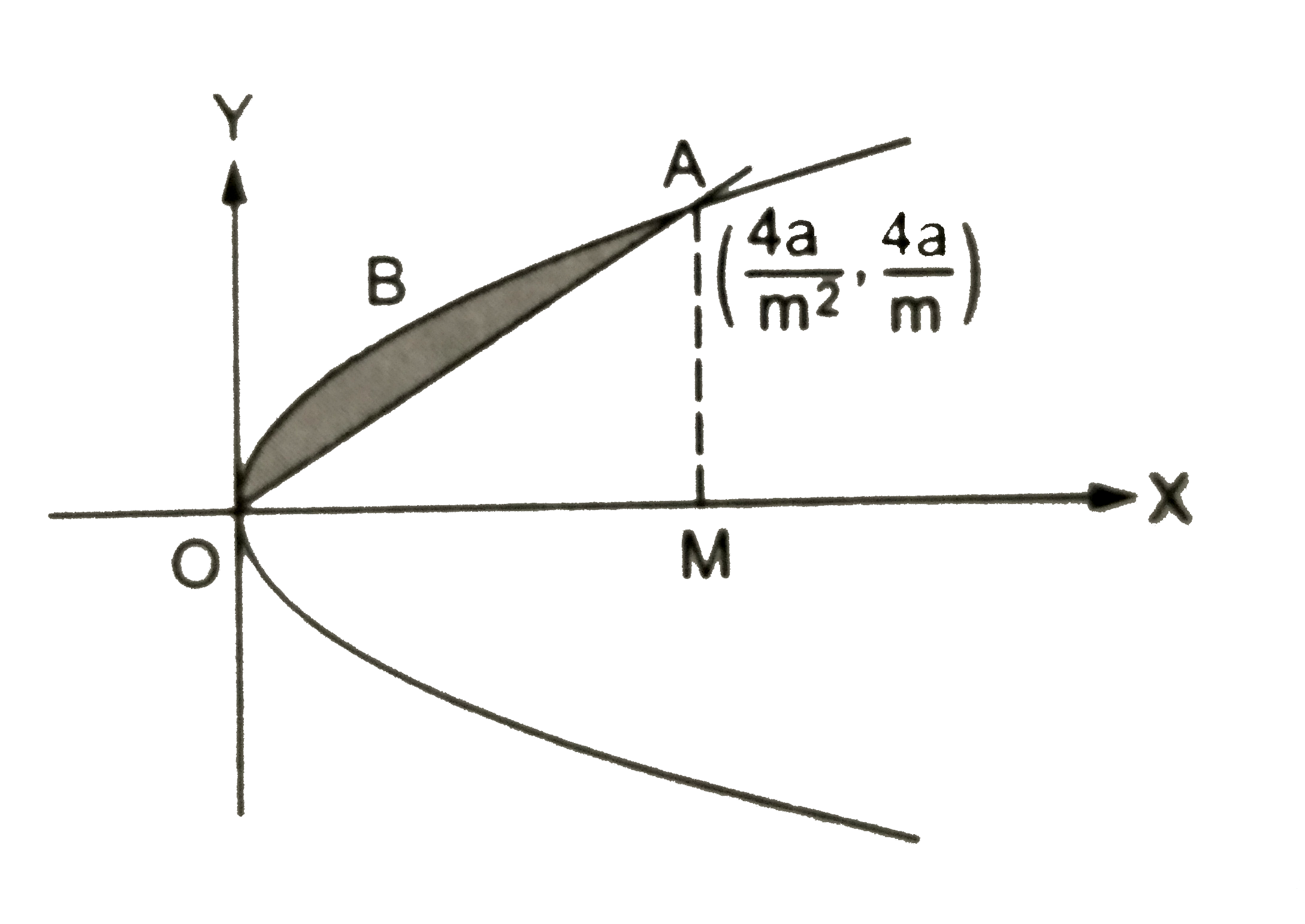
and y= mx ….(ii) Clearly $y^{2} = 4 a x$ is a right handed parabola passing through the origin And y=mx is a line passing through the origin .
In order to find points of intersection of the given parabola and putting y=mx from (ii) and (ii) simultaneously
Putting y=mx from (ii) into (i) we get
$m^{2} x^{2} = 4 a x \Rightarrow x (m^{2} x 4 a) = 0$
$m^{2} x^{2} j = 4 a x \Rightarrow x (m^{2} x - 4 a) = 0$
$\Rightarrow x = 0 or x = 4 \frac{a}{m^{2}}$
Now $(x = 0 \Rightarrow y = 0) and (x = \frac{4 a}{m^{2}} \Rightarrow y = \frac{4 a}{m})$
So , the points of intersection of the given parabola and the chord are
$O (0, 0) and A (\frac{4 a}{m^{2}}, \Rightarrow y = \frac{4 a}{m})$
Draw $A M ⊥ O X$
Required area = (area OBAMO)=(area OAMO)
$= 4 a / m^{2} \int 0$ (y for the parabola ) dx- $= 4 a / m^{2} \int 0$ (y for the line )dx
$= 4 a / m^{2} \int 0 2 \sqrt{a x} d x - = 4 a / m^{2} \int 0 m x d x$
$= 2 \sqrt{a} . \frac{2}{3} {[x^{3 / 2}]}_{0}^{3 / 2} - {[\frac{m x^{2}}{2}]}_{0}^{4 a / m^{2}}$
$= [\frac{4 \sqrt{2}}{3} . \frac{8}{m^{3}} a^{3 / 2} - \frac{m}{2} . \frac{16 a^{2}}{m^{4}}]$
$= (\frac{32 a^{2}}{3 m^{2}} - \frac{8 a^{2}}{m^{3}}) = (\frac{8 a^{2}}{3 m^{2}})$ sq units
Hence , the required area is $(\frac{8 a^{2}}{3 m^{2}})$ sq units .

If the area enclosed between the parabola $y^{2} = 4 x$ and the line y = mx is (1/3) sq. unit, then : m =
A1
B2
C3
D4
Area between the parabola $y^{2} = x$ and the line x = 3 is
A $4 \sqrt{3}$
B $2 \sqrt{3}$
C $6 \sqrt{3}$
D $5 \sqrt{3}$
The area between the parabola $y = x^{2}$ and the line y=x is :
A $\frac{1}{6}$ sq unit
B $\frac{1}{3}$ sq unit
C $\frac{1}{2}$ sq unit
Dnone of these