Find the area of a quadrilateral ABCD in which AD=24cm, ∠BAD=900and BCD from an equilateral triangle whose each side is equal to 26cm.
To find the area of quadrilateral ABCD, we will break it down into two triangles: triangle ABD and triangle BCD.
1. Identify the Given Information:
- Length of AD = 24 cm
- Angle BAD = 90°
- Triangle BCD is equilateral with each side = 26 cm.
2. Find the Length of AB:
- In triangle ABD, we can use the Pythagorean theorem since it is a right triangle.
- We know:
AB2+AD2=BD2
- Here, BD=BC=26cm (since BCD is equilateral).
- Substitute the values:
AB2+242=262
AB2+576=676
AB2=676−576=100
AB=√100=10cm
3. Calculate the Area of Triangle ABD:
- The area of a right triangle is given by:
Area=12×base×height
- Here, base = AB = 10 cm and height = AD = 24 cm.
- Thus,
AreaABD=12×10×24=120cm2
4. Calculate the Area of Triangle BCD using Heron's Formula:
- First, find the semi-perimeter s:
s=AB+BC+CD2=26+26+262=39cm
- Now, apply Heron's formula:
Area=√s(s−a)(s−b)(s−c)
- Here, a=26cm,b=26cm,c=26cm:
AreaBCD=√39(39−26)(39−26)(39−26)=√39×13×13×13
=√39×133=√39×2197=√85803
=132×√3=169√3≈292.72cm2
5. Calculate the Total Area of Quadrilateral ABCD:
- Combine the areas of triangles ABD and BCD:
AreaABCD=AreaABD+AreaBCD=120+292.72=412.72cm2
Final Answer:
The area of quadrilateral ABCD is approximately 412.72cm2.
- Length of AD = 24 cm
- Angle BAD = 90°
- Triangle BCD is equilateral with each side = 26 cm.
- In triangle ABD, we can use the Pythagorean theorem since it is a right triangle.
- We know:
AB2+AD2=BD2
- Here, BD=BC=26cm (since BCD is equilateral).
- Substitute the values:
AB2+242=262
AB2+576=676
AB2=676−576=100
AB=√100=10cm
- The area of a right triangle is given by:
Area=12×base×height
- Here, base = AB = 10 cm and height = AD = 24 cm.
- Thus,
AreaABD=12×10×24=120cm2
- First, find the semi-perimeter s:
s=AB+BC+CD2=26+26+262=39cm
- Now, apply Heron's formula:
Area=√s(s−a)(s−b)(s−c)
- Here, a=26cm,b=26cm,c=26cm:
AreaBCD=√39(39−26)(39−26)(39−26)=√39×13×13×13
=√39×133=√39×2197=√85803
=132×√3=169√3≈292.72cm2
- Combine the areas of triangles ABD and BCD:
AreaABCD=AreaABD+AreaBCD=120+292.72=412.72cm2
The area of quadrilateral ABCD is approximately 412.72cm2.
Topper's Solved these Questions
Similar Questions
Find the area of a quadrilateral ABCD in which AD=24cm, ∠BAD=900and BCD from an equilateral triangle whose each side is equal to 26cm.
View SolutionIn a cyclic quadrilateral ABCD, if AB ∣∣ CD and ∠B=70∘, find the remaining angles.
View SolutionIf the diagonals AC,BD of a quadrilateral ABCD, intersect at O, and seqarate the quadrilateral into four triangles of equal area, show that quadrilateral ABCD is a parallelogram. GIVEN : A quadrilateral ABCD such that its diagonals AC and BD intersect at O and separate it into four parts such that ar(AOB)=ar(BOC)=ar(COD)=ar(AOD) TO PROVE : Quadrilateral ABCD is a parallelogram.
View SolutionThe diagonals of quadrilateral ABCD,ACandBD intersect in O. Prove that if BO=OD, the triangles ABCandADC are equal in area.
View SolutionCalculate the area of the quadrilateral ABCD as shown in Fig.33, given that BD=42 cm , AC=28 cm , OD=12 cm and AC⊥BD .
View SolutionIn a quadrilateral ABCD , given that ∠A+∠D=90o . Prove that AC2+BD2=AD2+BC2 .
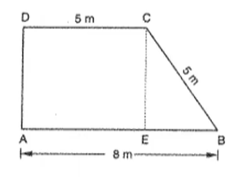
View SolutionIn quadrilateral ABCD show in Figure. ABDC and AD⊥AB. Also, AB=8m, DC=BC=5m. Find the area of the quadrilateral.
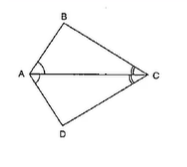
View SolutionIn Figure, diagonal AC of a quadrilateral ABCD bisects the angles A and C . Prove that AB=AD and CB=CD
View SolutionIn Figure, ABCD is a rectangle in which CD=6cm,AD=8cm Find the area of parallelogram CDEF

View SolutionIn Figure, ABCD is a quadrilateral in which diagonal AC=84 cm ; DL⊥AC, BM⊥AC, DL=16.5 cm and BM=12 cm . Find the area of quadrilateral ABCD.
View Solution
