Find the area of region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
Video Solution
Text Solution
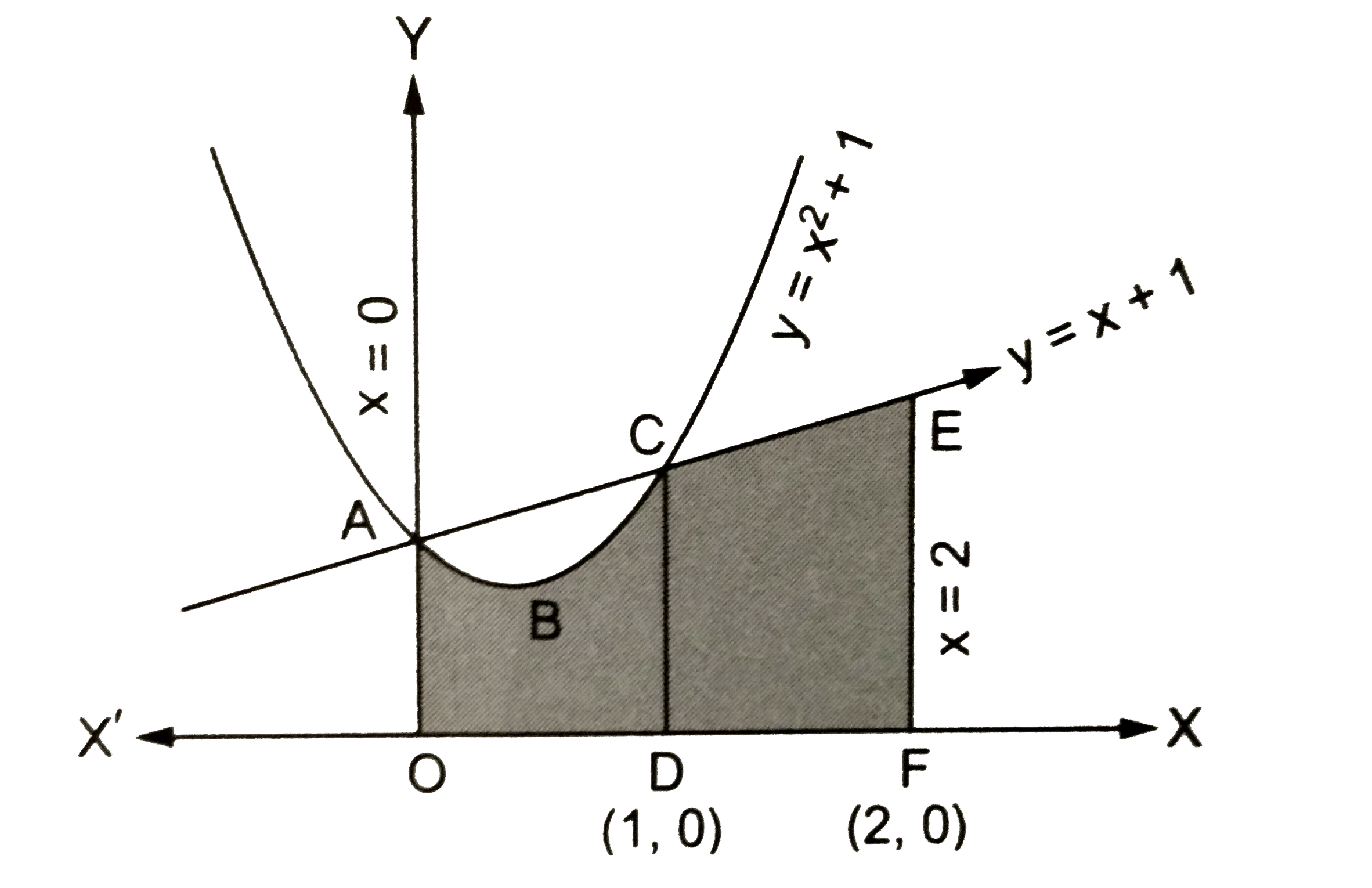
Let R ={(x,y):0≤y≤(x2+1),0≤y≤(x+1),0≤x≤2}
={(x,y):0≤y≤(x2+1)}∩{(x,y):0≤y≤(x+1)}∩{(x,y):0≤x≤2}
=R1∩R2∩R3.
Clearly , R1 is the region consisting of the right-hand side of the y-axis , lying below the parabola y=x2+1.
Also ,R2 is the region consisting of the right-hand side of the y-axis , lying below the line y = (x + 1)
And R3 is the region above the axis , lying between the ordinates x = 0 and x = 2
Thus R1∩R2∩R2∩R3 is the shaded region .
We have , y=x2+1 and y = x + 1
⇒x2+1=x+1⇒x(x−1)=0⇒x=0 or x = 1
Now , (x=0⇒y=1) and (x=1⇒y=2).
Thus , the parabola y=(x2+1) and the line y = x + 1 intersect at the points A (0,1) and C(1,2) .
∴ required area = area of the shaded region
= (area ODCBA) + (area CDFEC)
= 1∫0 (y of the parabola ) dx + 2∫1(y of the line ) dx
=1∫0(x2+1)dx+2∫1(x+1)dx
=[x33+x]10+[x22+x]21
=(13+1)+(4−32)=236 sq units .
Hence the required area is 236 sq units
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
The area of region{(x,y):x2+y2≤1≤x++y} is
Aπ25sq unitsBπ22sq unitsCπ24sq unitsD(π4−12) sq unitsIf the line x=α divides the area of region R={(x,y)∈R2:x0≤y≤x,0≤x≤1} into two equal parts, then
A2α4−4α2+1=0Bα4+4α2−1=0C12<α<1D0<α≤12If the line x=α divides the area of region R={(x,y)∈R2:x3≤y≤x,0≤x≤1} into two equal parts, then
A2α4−4α2+1=0Bα4+4α2−1=0C12<α<1D0<α≤12
