Question

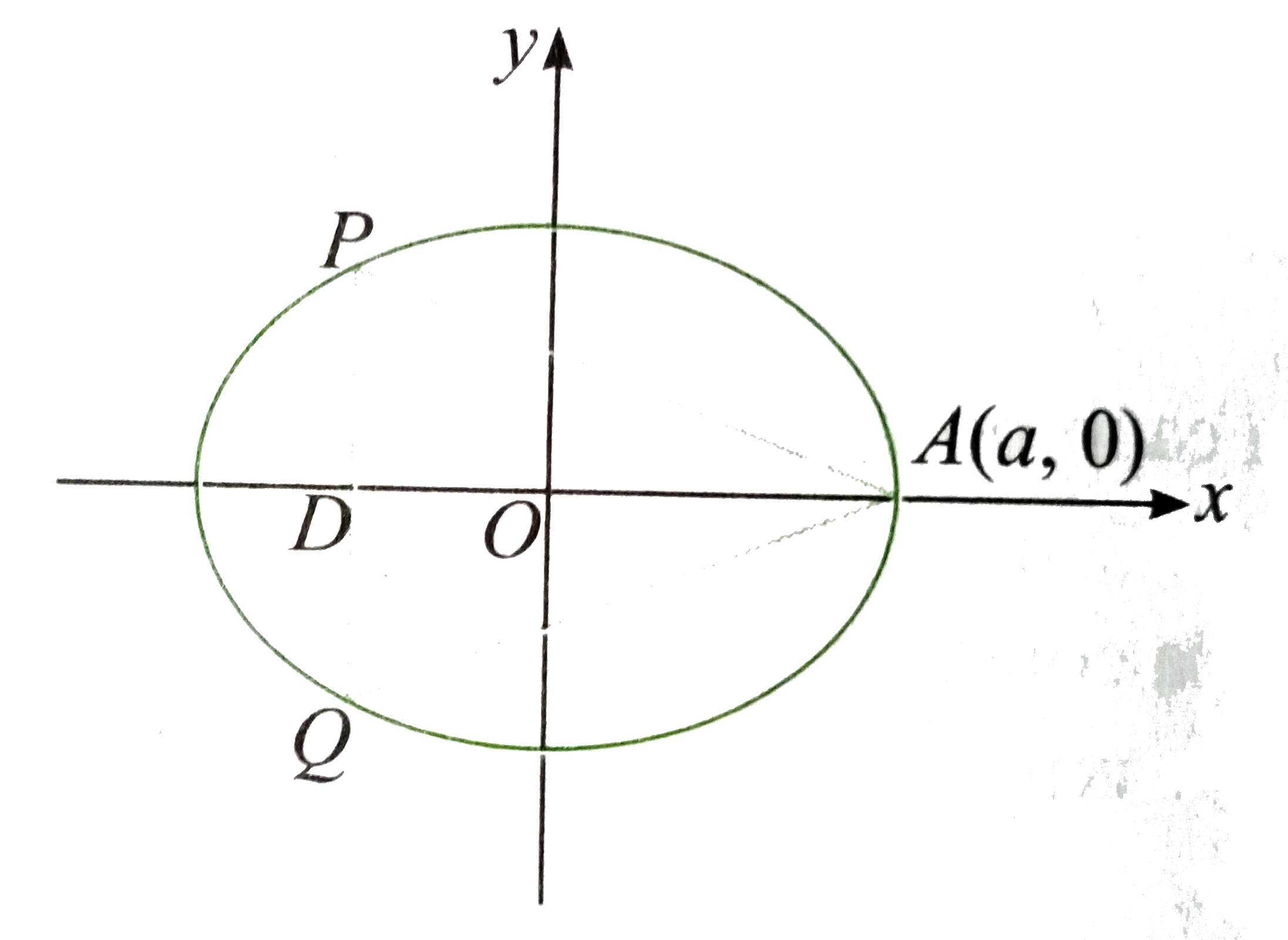
Find the area of the greatest isosceles triangle
that can be inscribed in the ellipse ${\displaystyle \left(\frac{x^2}{a^2}\right)+\left(\frac{y^2}{b^2}\right)=1}$
having its vertex coincident with one extremity of the
major axis.

Explanation

Let APQ be the isoceles triangle inscribed in the ellipse `(x^(2)//a^(2))+(y^(2)//b^(2))=1` with one vertex A at the extermity (a,0) of the major axis. If the coordinates of P are `(a cos theta, -b sin theta)` then those of Q will be `(acos theta b- sin theta)`,
So, area of `DeltaAPQ`. is given by
`Delta=(1)/(2)PQ*AD`
`=PD*AD`
`=PD(OA+OD)`
`= b sin theta (a-a cos theta)`
`=(1)/(2)ab(2 sin theta-sin 2theta),0lt thetalepi`

`:. (dDelta)/(Delta theta)=ab(cos theta-cos 2theta)`
and
`(d^(2)Delta)/(d theta^(2))=ab(-sin theta+2 sin 2 theta)`
For maximum or minimum of `Delta`.
`(dDelta)/(d theta)=0`
`or costheta-cos2theta=0`
`or 2 cos^(2)theta-cos theta-1=0`
or ` (2costheta+1)(cos theta-1)=0`
`or cos theta=(1)/(2)" " ( :. cos theta ne 1 as thetane0)`
or `theta=(2pi)/(3)`
Whern `theta=2pi//3`, we have
`(d^(2)Delta)/(d theta^(2))=-(1)/(2)(3sqrt(3))ab,(-ve)`
Therfore the area is maximum when `theta =2pi//3`
Therefore, maximum area
`Delta=(1)/(2)ab[2sin.(2pi)/(3)-sin.(4pi)/(3)]`
`=(1)/(4)(3sqrt(3))ab`