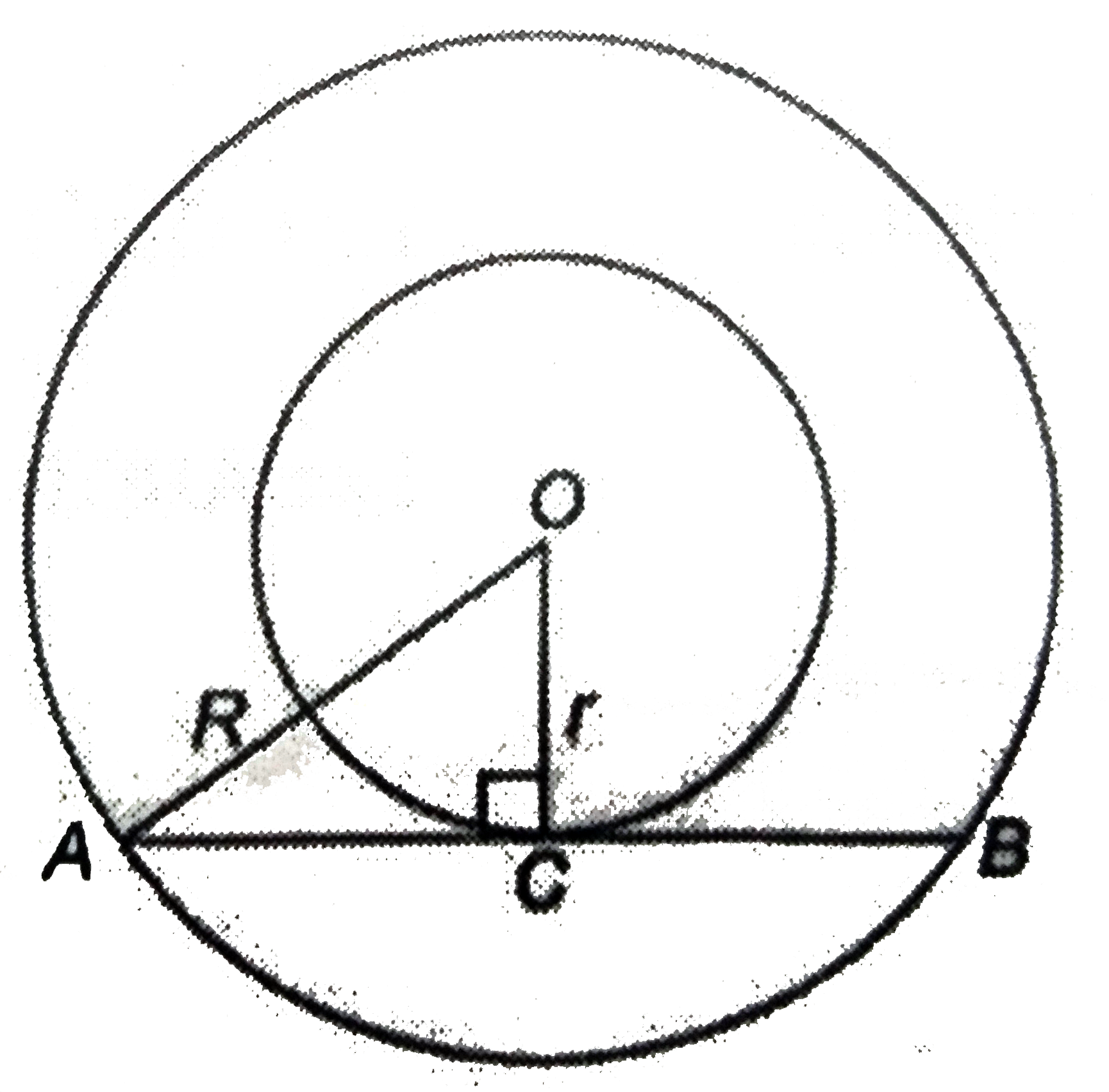
Find the area of the region between the two concentric circles, if the length of a chord of the outer circle just touching the inner circle at a particular point on it is 10 cm (Take, $π = \frac{22}{7}$ )

Video Solution

Text Solution

Verified by Experts

Let the chord AB touch the inner circle at C and let O be the centre of both the circles, then
$O C = r, O A = R and A B = 10 c m$
Now, since $O C ⊥ A B$ ( $∵$ radius through point of contact is perpendicular to the tangent)
$∴$ C is the mid-point of AB
( $∵ ⊥$ drawn from the centre of the chord, bisects the chord)
$\Rightarrow A C = \frac{1}{2} A B = \frac{1}{2} \times 10 = 5 c m$
Now, in right $Δ O C A$
$O A^{2} = O C^{2} + A C^{2}$ (by Pythagoras theorem)
$\Rightarrow R^{2} - r^{2} = 25$ ...(1)
$∴$ The required area of region between two concentric circle
$= π R^{2} - π r^{2} = π (R^{2} - r^{2}) = 25 π$ [from (1)]
$= 25 \times \frac{22}{7} = 78.57 c m^{2}$

Updated on:21/07/2023

In two Concentric circles, AB and CD are two chords of the outer circle which touch the inner circle at E and F. Then :
AAB = CD
B $A B = \frac{1}{2} C D$
C $A B \neq C D$
DNone of these
Two concentric circles are of radii 13 cm and 5 cm. The length of the chord of the larger circle which touches the smaller circle is:
दो संकेंद्री वृत्तों की त्रिज्या 13 सेमी तथा 5 सेमी है। बड़े वृत्त की जीवा की लंबाई ज्ञात कीजिए, जो छोटे वृत्त को स्पर्श करती है।
A6 cm
B7 cm
C10 cm
D8 cm