Find the area of the region bounded by the curve $C : y = tan x, t a n \geq n t d r a w n \to C$ at $x = \frac{π}{4},$ and the x-axis.

Video Solution

Text Solution

Verified by Experts

The given curve is $y = tan x (1)$
$When x = π / 4, y = 1$
i.e., co-ordinates of P are $(π / 4, 1)$
$∴ equation of tangent at P is y - 1 = ({sec}^{2} \frac{π}{4}) (x - π / 4)$
$or y = 2 x + 1 - π / 2$
The graphs of (1) and (2) are as shown in the figure.

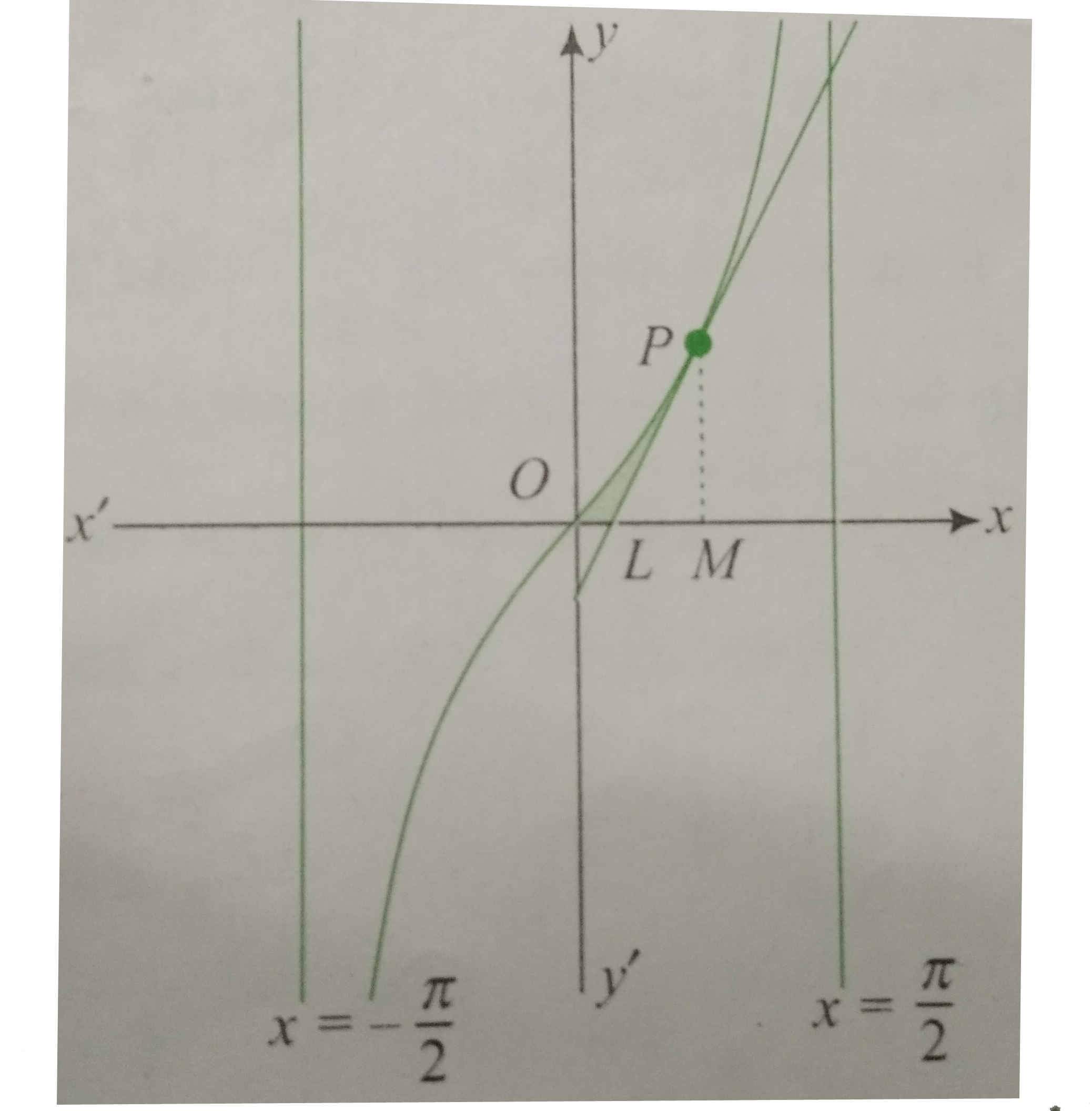
$Tangent (2) meets x-axis at L (\frac{π - 2}{4}, 0)$
Now, Required area =Shaded area
$= Area O P M O - A r (Δ P L M)$
$= \int_{0}^{π / 4} tan x d x - \frac{1}{2} (O M - O L) P M$
$= {[log sec x]}_{0}^{π / 4} - \frac{1}{2} \times {\frac{π}{2} - \frac{π - 2}{4}} \times 1$
=(1)/(2)[ log 2 -(1)/(2)]sq. units.

Updated on:21/07/2023