Question

Find the area
of the region bounded by the parabola ${\text{x}}^2=4\text{y}$
and the line $\text{x}=4\text{y}-2$

Explanation

The given curve is `x^2 =4y `
The given line is x=4y -2

Putting 4y= (x+2) from (ii) into (i) we get
`x^2= (x+2) iff (x^2 -x-2)=0`
`iff (x-2) (x+1) =0`
`iff x=2 or x =-1`
Putting x =2 in (i) we get y=-1
Putting x =-1 in (i) weget `y=1/4`
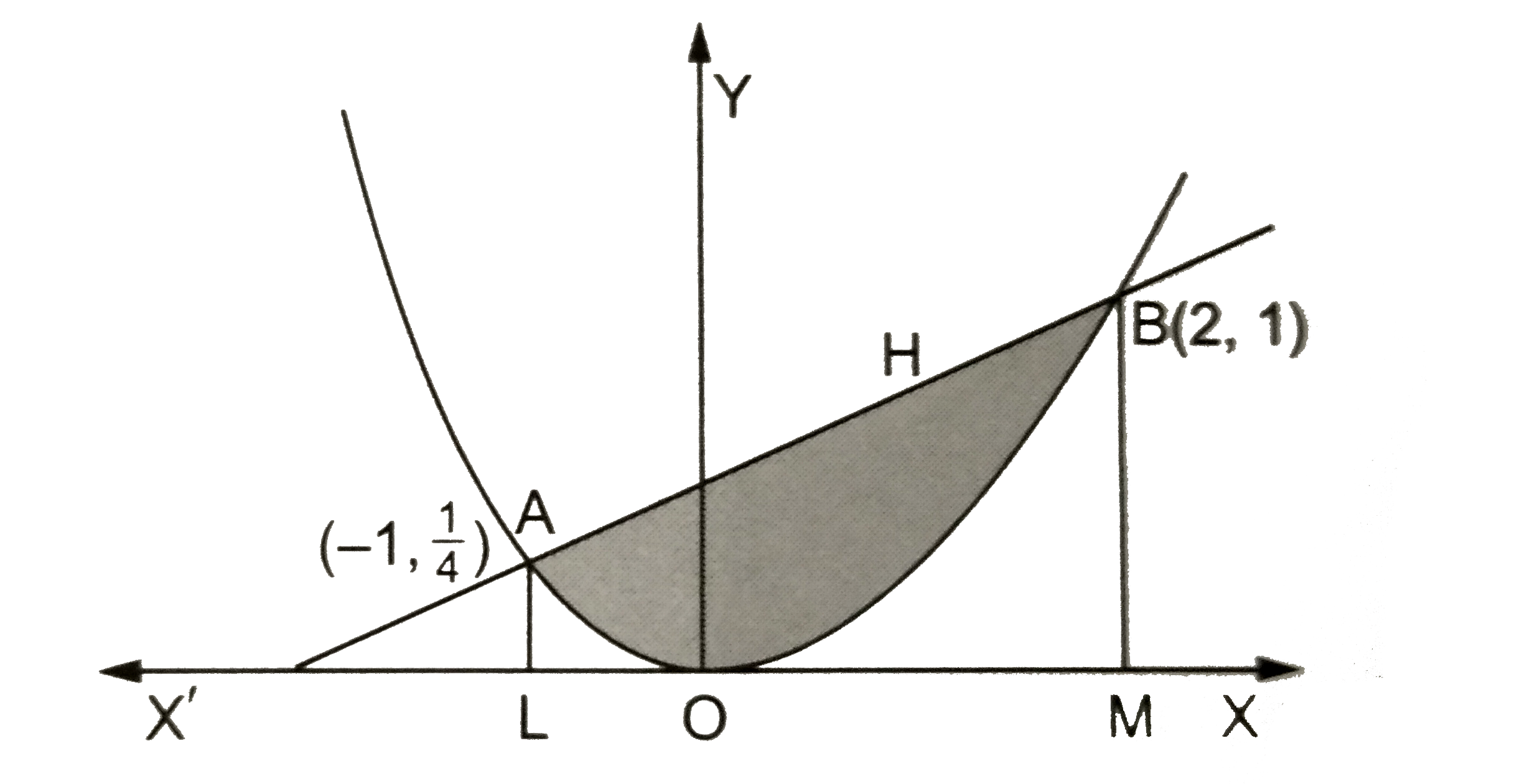
Thus the points of intersection of the given curve (i) and the line (ii) are `A(-1,1/4)` and B (2,1)
Draw AL and BM are perpendiculars on the x-axis
`therefore` required are= area AOBA
=(area ALMBA )- (area AOMLA)
`underset(-1)overset(2)int((x-2)/(4))dx-underset(-1)overset(2)int(x^2)/(4) d x `
`=underset(-1)overset(2)int{((x+2)/(4))-(x^2)/(4)}dx=1/4[x^2/2+2x =x^3/3]_-1 ^2`
`1/4[(2+4-8/3)-(1/2-2+1/3)]=9/8`sq units