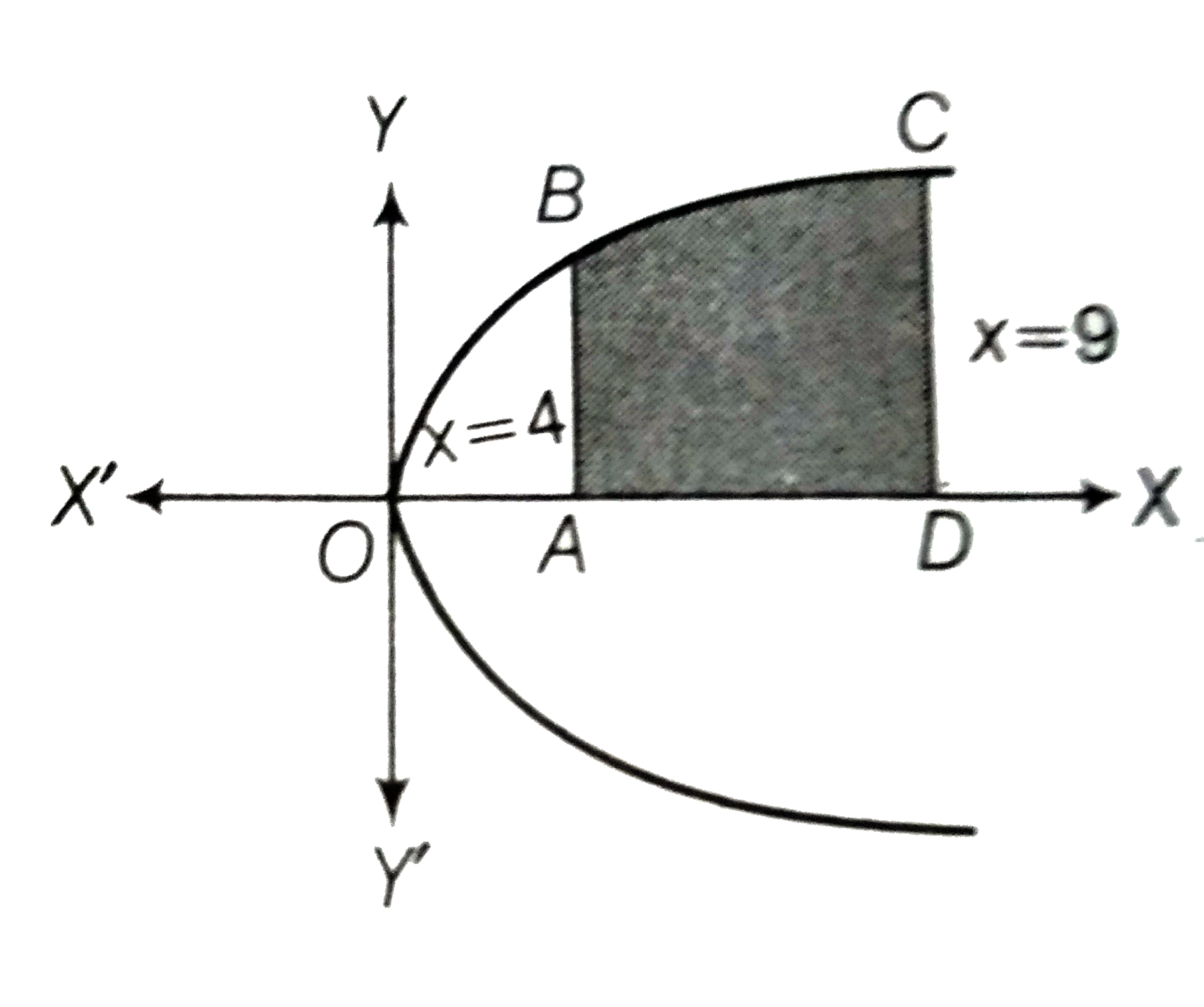
Find the area of the region bounded by the parabola $y^{2} = 4 a x$ , its axis and two ordinates $x = 4$ and $x = 9$

A

$\frac{86 \sqrt{b}}{3}$ sq units

B

$\frac{76 \sqrt{a}}{3}$ sq units

C

$\frac{92 \sqrt{a}}{4}$ sq units

D

$\frac{93 \sqrt{b}}{3}$ sq units

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Given equation of parabola is $y^{2} = 4 a x$ , its axis is Y = 0 and vertex is (0, 0). Also, given ordinates x = 4 and x = 9. The bounded region in I quadrant is ABCDA.
$∴$ Required area
$= \int_{4}^{9} y d x = \int_{4}^{9} \sqrt{4 a x} d x [∵ y^{2} = 4 a ξ m p l i e s y = \sqrt{4 a x}, as y is in I quadranr]$
$= 2 \sqrt{a} \int_{4}^{9} \sqrt{x} d x = 2 \sqrt{a} {[\frac{x^{3 / 2}}{3 / 2}]}_{4}^{9}$
$= 2 \sqrt{a} \times \frac{2}{3} [{(9)}^{3 / 2} - {(4)}^{3 / 2}]$
$= \frac{4}{3} \sqrt{a} [{(3^{2})}^{3 / 2} - {(2^{2})}^{3 / 2}]$
$= \frac{4}{3} \sqrt{a} [27 - 8] = \frac{4}{3} \sqrt{a} (19) = \frac{76}{3} \sqrt{a}$ sq unit
Hence, the required area is $\frac{76 \sqrt{a}}{3}$ sq unit.

|

Class 12 MATHS APPLICATION OF INTEGRALS

Topper's Solved these Questions

Similar Questions

MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERS-APPLICATIONS OF DEFINITE INTEGRALS -MHT CET Corner

Home
Ask Doubt
Profile