Find the area of the region bounded by the points (3,0),(4,5)and(5,1).
The correct Answer is:92sq. units
To find the area of the region bounded by the points (3,0), (4,5), and (5,1), we can use the formula for the area of a triangle given its vertices. The formula for the area A of a triangle with vertices at coordinates (x1,y1), (x2,y2), and (x3,y3) is given by:
A=12|x1(y2−y3)+x2(y3−y1)+x3(y1−y2)|
Step 1: Identify the coordinates
We have the points:
- A(3,0) → (x1,y1)
- B(4,5) → (x2,y2)
- C(5,1) → (x3,y3)
Step 2: Substitute the coordinates into the formula
Now we substitute the coordinates into the area formula:
A=12|3(5−1)+4(1−0)+5(0−5)|
Step 3: Simplify the expression
Calculating each term inside the absolute value:
1. 3(5−1)=3×4=12
2. 4(1−0)=4×1=4
3. 5(0−5)=5×(−5)=−25
Now, combine these results:
A=12|12+4−25|
A=12|16−25|=12|−9|=12×9=92
Step 4: Final result
Thus, the area of the triangle formed by the points (3,0), (4,5), and (5,1) is:
92 square units
We have the points:
- A(3,0) → (x1,y1)
- B(4,5) → (x2,y2)
- C(5,1) → (x3,y3)
Now we substitute the coordinates into the area formula:
Calculating each term inside the absolute value:
2. 4(1−0)=4×1=4
3. 5(0−5)=5×(−5)=−25
Thus, the area of the triangle formed by the points (3,0), (4,5), and (5,1) is:
Topper's Solved these Questions
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - QUESTIONS FROM NCERT BOOK (EXERCISE 8.1)
13 Videos
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - QUESTIONS FROM NCERT BOOK (EXERCISE 8.2)
7 Videos
- APPLICATIONS OF THE INTEGRALS BOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF THE INTEGRALS EXERCISE - OBJECTIVE TYPE QUESTIONS -TRUE/FALSE
5 Videos
- APPLICATIONS OF DERIVATIVESBOOK - MODERN PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - CHAPTER TEST (1)
12 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - MODERN PUBLICATIONCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - CHAPTER TEST
12 Videos
Similar Questions
Using integration, find the area of the region bounded by :
(i)(1,0),(4,5)and(6,3)
(ii) (1,0),(2,2)and(3,1)
(iii)(−1,2),(1,5)and(3,4)
(iv) (2,3),(3,5)and(3,4)
(v) (−1,0),(1,3)and(3,2)
(vi) (1,3),(2,5)and(3,4)
(vii) (4,1),(6,6)and(8,4)
(viii) (2,5),(4,7)and(6,2)
(ix) (−2,1),(0,4)and(2,3)
(x) (2,1),(3,4)and(5,2).
View SolutionFind the area of the region bounded by the parabola y2=25x and the line x =5
View Solution
Knowledge Check
Find the area of the region bounded by the ellipse x24+y29=1.
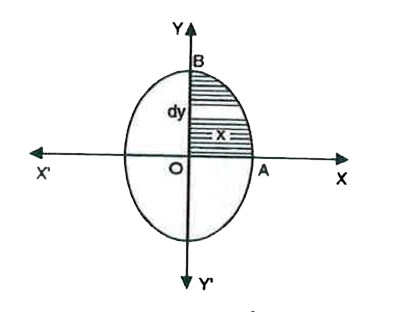 A10πB11πC12πD13π
A10πB11πC12πD13π
Find the area of the region bounded by the parabola x2=4y and The X-axis & the line x = 1, x = 4.
View SolutionFind the area of the region bounded by the curve y=x3,y=x+6 and x=0
View SolutionFind the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=1andx=1.
View SolutionFind the area of the region bounded by the line y=3x+2, the x-axis and the ordinates x=−1 and x=1
View SolutionFind the area of the region bounded by the curves y=x2+2, y=x,x=0andx=3.
View SolutionFind the area of the region bounded by the curves y=x2+2y=x,x=0,andx=3.
View SolutionFind the area of the region bounded by y=x4,x=1,x=5 and x-axis.
View Solution
