Find the area of the region bounded by the two parabolas y=x2and y2=x.
Clearly x2=y is an upward parabola with is vertex at (0,0) and y2=x is right -handed parabola with its vertex also at (0,0).The shaded region shows the area bounded by these parabolas.
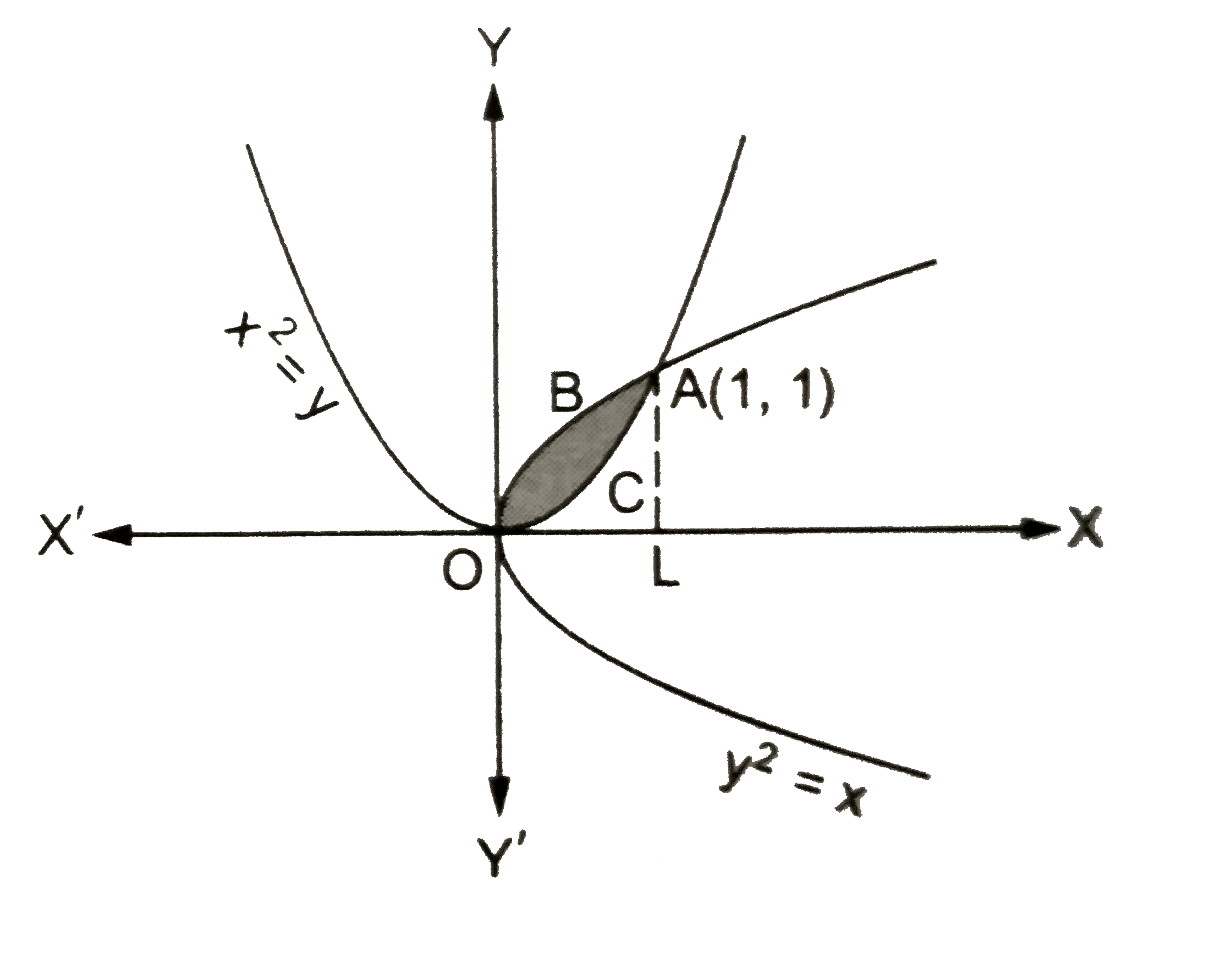
The given equations are
x2=y
and y2=x
Using (i) in (ii) we get
x4=x⇒(x3−1)=0⇒x=0orx=1
Also (x=0⇒y=0)and(X=1⇒y=1)
So , the given curves intersect at O (0,0) and A(1,1)
Draw AL⊥OX
Required area =(area OLABO)-(area OLACO)
= (area bounded by x2=y from x =0 to x=1}
=1∫0√x dx −1∫0x2dx
=[23x3/2]10−[x33]10=(23−13)=13 sq unit.
Hence , the required area is 13 sq unit
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 1739videos
AREA OF BOUNDED REGIONS
- BOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions89videos
APPLICATIONS OF DERIVATIVES
- BOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 3018videos
BAYES'S THEOREM AND ITS APPLICATIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
What is the area of the region bounded by the parabola y2=6(x−1) and y2=3x?
AA. √63BB. 2√63CC. 4√63DD. 5√63
Using integration calculate the area of the region bounded by the two parabolas y=x2 and x=y2
View SolutionFind the area of the region given by :
{(x,y):x2≤y≤|x|}.
(ii) Find the area bounded by thte curves :
{(x,y):y≥x2andy=|x|}.
(iii) Find the area of the region bounded by the parabola y=x2andy=|x|.View SolutionFind the area of the region bounded by: the parabola y=x2 and the line y=x
View SolutionIn what ratio does the x-axis divide the area of the region bounded by the parabolas y=4x−x2andy=x2−x?
View SolutionFind the area of the region bounded by the parabola y2=2px and x2=2py.
View SolutionDraw a rough sketch and find the area of the region bounded by the parabolas y2=4xandx2=4y, using the method of integration.
View SolutionFind the area of the region bounded by the parabola y2=4ax and the line x=a.
View Solution

