Find the area of the region enclosed between the two circles $x^{2} + y^{2} = 1$ and ${(x - 1)}^{2} + y^{2} = 1$

Video Solution

Text Solution

Verified by Experts

$(x^{2} + y^{2}) = 1$ is a circle with is its centre at (0,0) and radius =1 unit

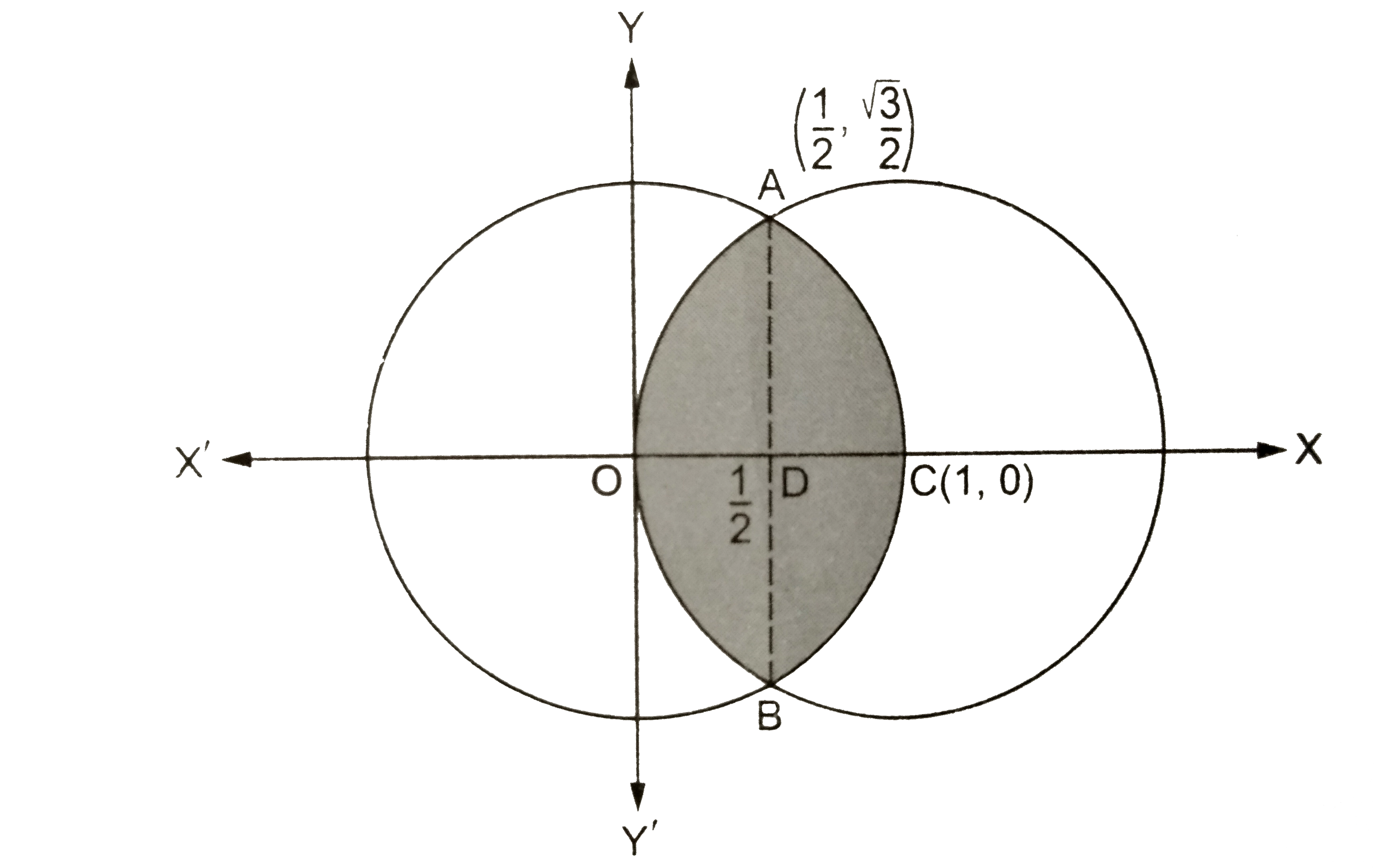
And ${(x - 1)}^{2} + y^{2} = 1$ is a circle with its centre at (1,0) and radius =1 unit.
The given equations are
$(x^{2} + y^{□}) = 1$
and ${(x - 1)}^{2} + y^{2} = 1$
Using (i) in (ii) ,we get 1-2x =0 $\Rightarrow x = \frac{1}{2}$
Putting $x = \frac{1}{2}$ in (i) ,we get $y = \pm \frac{\sqrt{3}}{2}$
So the two circles interset at A $(\frac{1}{2}, \frac{\sqrt{3}}{2}) and B (\frac{1}{2}, \frac{- \sqrt{3}}{2})$
Required area = area AOBCA
= 2 (area AOCA) =2 (area ODAO+ area DCAD )
$2 {\underset{0}{\int^{1 / 2}} \sqrt{1 - {(x - 1)}^{2}} d x + \underset{1 / 2}{\int^{1}} \sqrt{1 = x^{2}}}$

Updated on:21/07/2023