Find the area of the region in the first quadrant enclosed by x axis , the line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4 .$

Video Solution

Text Solution

Verified by Experts

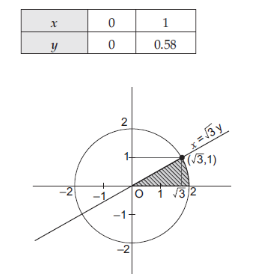
Obviously $x^{2} + y^{2} = 4$ is a
circle having centre at $(0, 0)$ and radius $2$ units.
For graph of line x $= \sqrt{3} y$
For intersecting point of given circle and line
putting $x = \sqrt{3} y in x^{2} + y^{2} = 4$
we get
${(\sqrt{3} y)}^{2} + y^{2} = 4$
$3 y^{2} + y^{2} = 4$
$4 y^{2} = 4$
$y = \pm 1$ , $y = \pm 1$
Intersecting points are $(\sqrt{3}, 1), (- \sqrt{3}, - 1)$
Shaded region is required region
Now required area $= \int_{0}^{\sqrt{3}} \frac{x}{\sqrt{3}} d x + \int_{\sqrt{3}}^{2} \sqrt{4 - x^{2}}$
$= \frac{1}{\sqrt{3}} {[\frac{x^{2}}{2}]}_{0}^{\sqrt{3}} + {[\frac{x \sqrt{4 - x^{2}}}{2} + \frac{4}{2} {sin}^{- 1} (\frac{x}{2})]}_{\sqrt{3}}^{2}$
$= \frac{1}{2 \sqrt{3}} (3 - 0) + [2 {sin}^{- 1} (1) - (\frac{\sqrt{3}}{2} + 2 {sin}^{- 1} (\frac{\sqrt{3}}{2})]$
$= \frac{\sqrt{3}}{2} + [2 (\frac{π}{2}) - \frac{\sqrt{3}}{2} - \frac{2 π}{3}]$
$= \frac{\sqrt{3}}{2} + π - \frac{\sqrt{3}}{2} - \frac{2 π}{3}$
$= π - \frac{2 π}{3} = \frac{π}{3}$ sq.unit

Conside the line $x = \sqrt{3} y$ and the circle $x^{2} + y^{2} = 4$
What is the area of the region in the first quadrant enclosed by the X-axis, the line $= \sqrt{3} y$ and the circle?
A $\frac{π}{3}$
B $\frac{π}{6}$
C $\frac{π}{3} - \frac{\sqrt{3}}{2}$
DNone of the above
Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle $x^{2} + y^{2} = 32$ is
A $16 π sq units$
B $4 π sq units$
C $32 π sq units$
D $24 π sq units$
Area of the region in the first quadrant exclosed by the X-axis, the line y=x and the circle $x^{2} + y^{2} = 32$ is
A $16 π sq units$
B $4 π sq units$
C $32 π sq units$
D $24 π sq units$