Find the area of the region in which the points satisfy the inequaties 4<x2+y2<16 and 3x2−y2>0Solution in Bengali
The points satisfying 4<x2+y2<16 lie in the region outside the circle x2+y2=4 and inside the circle x2+y2=16 as shown in the following figure.
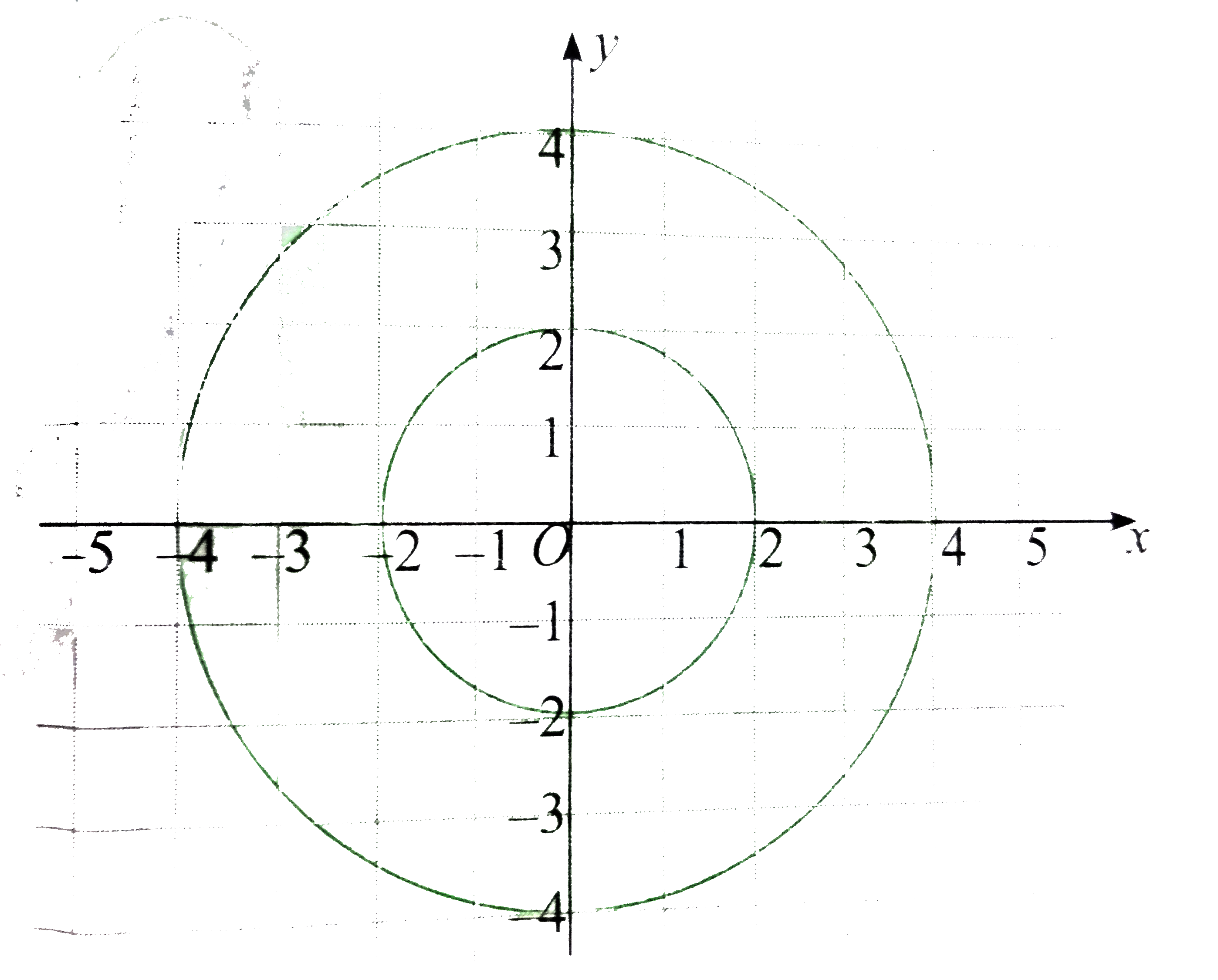
Now, 3x2−y2>0
∴(√3x−y)(√3x+y)>0
Now, draw the lines √3x−y=0 and √3x+y=0.
Therefore, 3x2−y2>0 represents the following region :
Hence, the region of the points satisfying both the inequalities is shown in the following figure.
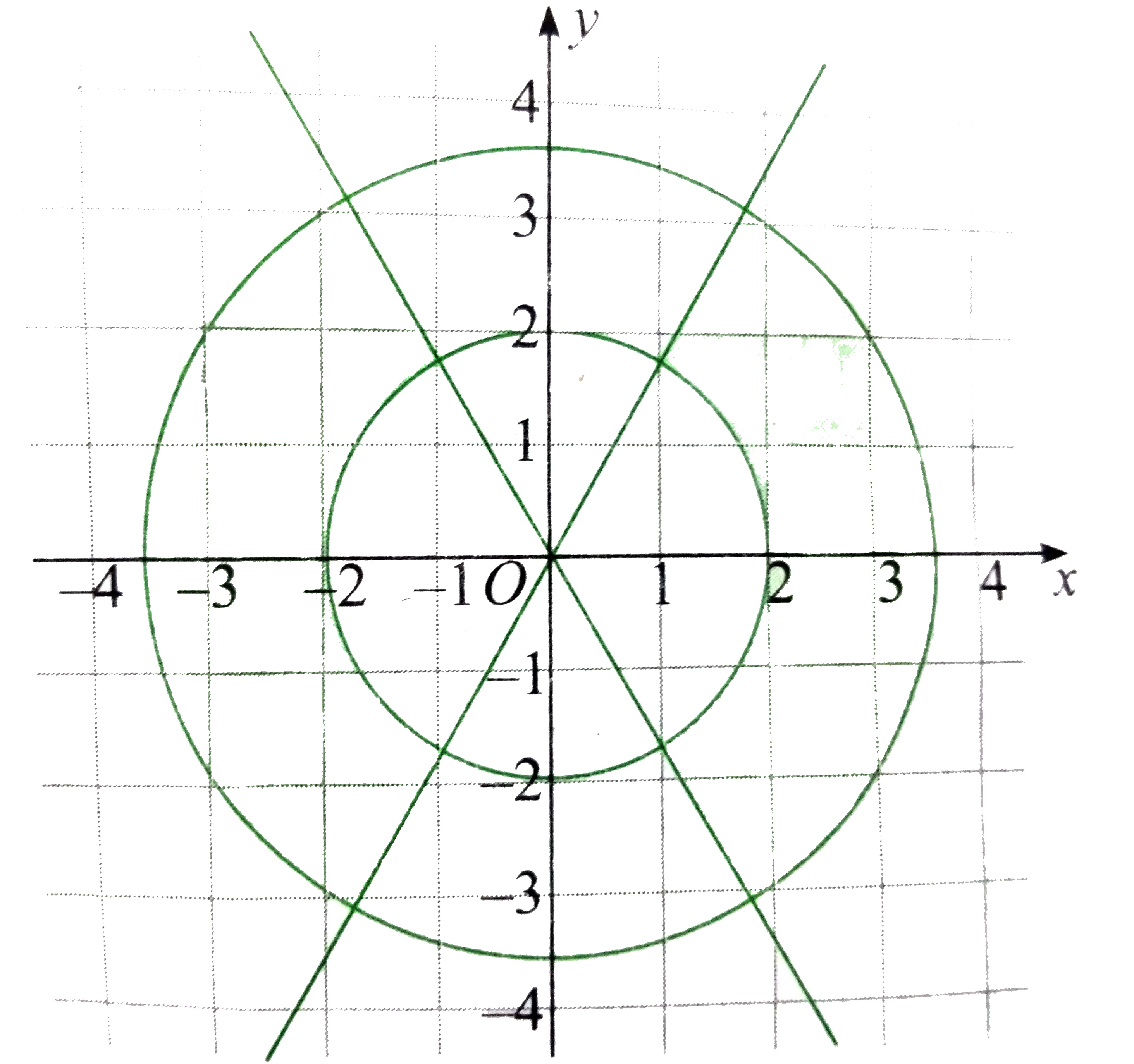
Hence, the required area is
46[π(4)2−π(2)2]=8π
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - Examples
13 Videos
- CIRCLE BOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLE EXERCISE - CONCEPT APPLICATION EXERCISE 4.1
1 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGE PUBLICATIONCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
The line Ax+By+C=0 cuts the circle x2+y2+ax+by+c=0 at PandQ . The line A′x+B′x+C′=0 cuts the circle x2+y2+a′x+b′y+c′=0 at RandS. If P,Q,R, and S are concyclic, then show that |a−a'b−b'c−c'ABCA'B'C'|=0
View SolutionIf a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View Solution
In the diagram as shown, a circle is drawn with centre C(1,1) and radius 1 and a line L. The line L is tangent to the circle at Q. Further L meets the y-axis at R and the x-axis at P in such a way that the angle OPQ equals θ where 0<θ<π2.
Coordinate of Q is
View SolutionFind the area of the region in which the points satisfy the inequaties 4<x2+y2<16 and 3x2−y2≥0.
View SolutionFind area of region bounded by y=x^(2)-3x+2,x=1,x=2 and y=0
View SolutionThe area of the region containing the points (x, y) satisfy-ing 4<=x^(2)+y^(2)<=2(|x|+|y|) is
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionFind the area of the region lying between the parabolas 4y2=9xand3x2=16y.
View SolutionFind the area of the region in which the points satisfy the inequaties 4<x2+y2<16 and 3x2−y2≥0.
View SolutionFind tha area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|).
View SolutionArea of region enclosed by the region y2≤3x,x2+y2≤4 and y≥0 is :
View SolutionDraw the rough sketch and find the area of the region : {(x,y):16x2+y2≤16,4x+y≥4}.
View SolutionFind the area of the region enclosed by the curves
y=x2andy=3x
View SolutionFind the area of the region bounded by the circles x2+y2=16 and (x+4)2+y2=16
View SolutionFind area of region bounded by y=x2–3x+2,x=1,x=2 and y=0.
View Solution
