Find the area of the region ${(x, y) : x^{2} + y^{2} \leq 2 a x$ , $y^{2} \leq a x$ , $x \leq 0$ , $y \leq 0}$

Video Solution

Text Solution

Verified by Experts

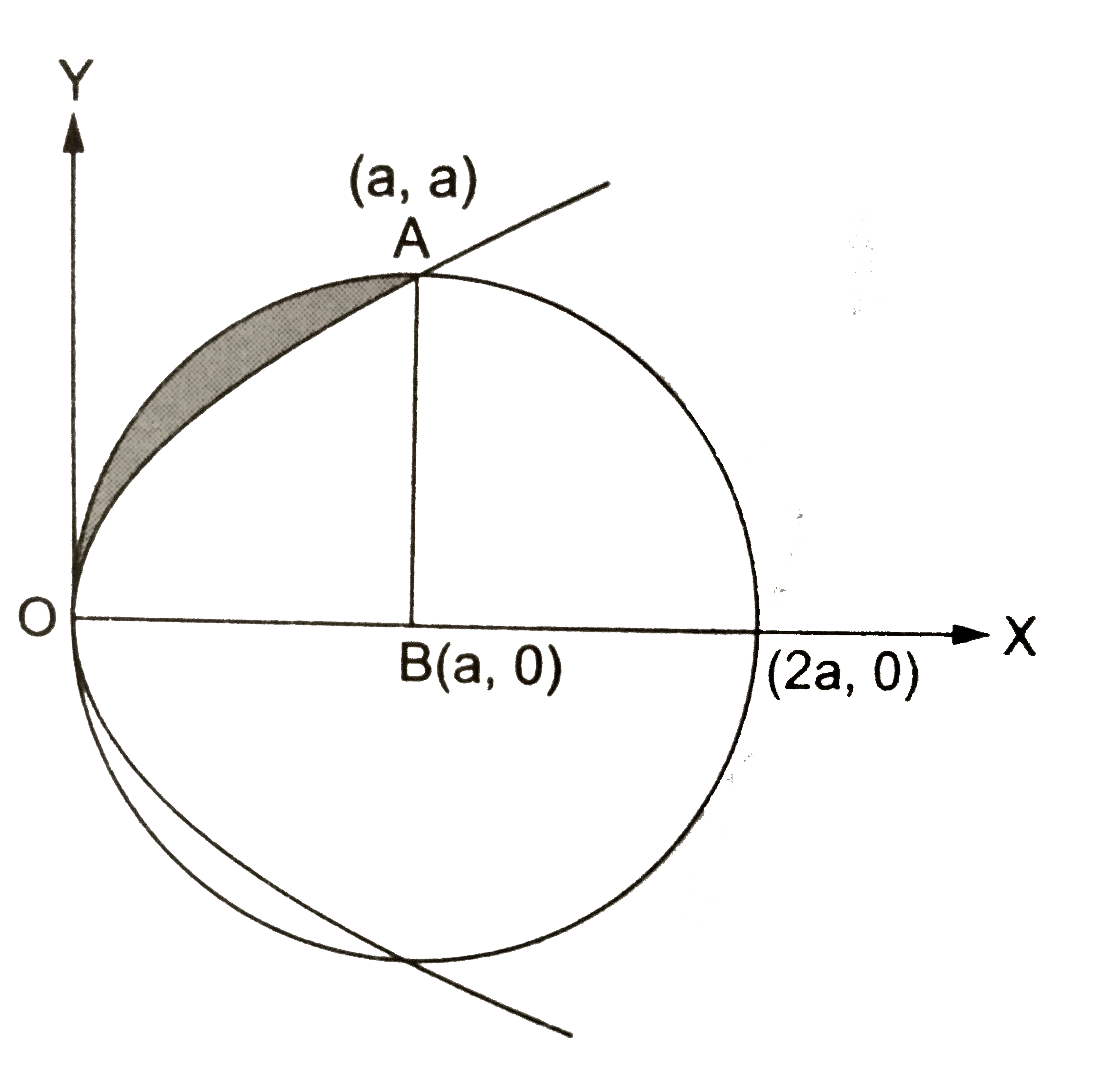
Clearly we have to find the area of the region lying in the first quadrant $(x \geq 0, y \geq 0)$ included between the circle $x^{2} + y^{2} = 2 a x$ and the parabola $y^{2} = a x$
Thus , the equations of the given curves are
$x^{2} + y^{2} = 2 a x \dots (i)$
and $y^{2} = a x$ ...(ii)
Now , clearly $x^{2} + y^{2} = 2 a x$ is a circle with its center $B (a, 0)$ and radius $= a$ units
And $y^{2} = a x$ is parabola with $O (0, 0)$ as its vertex and the x-axis as its axis. We can draw its figure as shown .
Their points of intersection may be obtained by solving $(i)$ and $(i i)$ and keeping in view that $x \geq 0 and y > 0$
Using $(i i)$ in $(i)$ ,we get
$x^{2} - a x = 0 \Rightarrow x (x - a) = 0$
$\Rightarrow x = 0 or x = a$
Now $(x = 0 \Rightarrow y = 0)$ and $(x = a \Rightarrow y = a)$
Thus, two curves intesect at O(0,0) and A(a,a)
$∴ required area = a \int 0 \sqrt{2 a x - x^{2}} d x - a \int 0 \sqrt{a x} d x$
$= a \int 0 \sqrt{a^{2} - {(x - a)}^{2}} d x - \sqrt{a} . a \int 0 \sqrt{x} d x$
$= {⎡ ⎢ ⎢ ⎣ \frac{(x - a) \sqrt{a^{2} - {(x - a)}^{2}}}{2} + \frac{a^{2}}{2} {sin}^{- 1} (\frac{x - a}{a}) ⎤ ⎥ ⎥ ⎦}_{0}^{a} - \sqrt{a} {[\frac{2}{3} x^{3 / 2}]}_{0}^{3 / 2}$
$= {\frac{a^{2}}{2} {sin}^{- 1} (0) - \frac{a^{2}}{2} {sin}^{- 1} (- 1) - \frac{2}{3} a^{2}}$
$= (\frac{π a^{2}}{4} - \frac{2}{3} a^{2})$ sq units
Hence, the required area is $= (\frac{π a^{2}}{4} - \frac{2}{3} a^{2})$ sq units .

The area of the region ${(x, y) : x^{2} + y^{2} \leq 1 \leq x + y}$ , is
A $\frac{π}{5}$
B $\frac{π}{4}$
C $\frac{π^{2}}{4}$
D $\frac{π}{4} - \frac{1}{2}$
The area of region ${(x, y) : x^{2} + y 2 \leq 1 \leq x + + y}$ is
A $\frac{π^{2}}{5}$ sq units
B $\frac{π^{2}}{2}$ sq units
C $\frac{π^{2}}{4}$ sq units
D $(\frac{π}{4} - \frac{1}{2})$ sq units
The area of the region ${(x, y) : x y \leq 8, 1 \leq y \leq x^{2}}$ is :
A $8 {log}_{e} 2 - \frac{14}{3}$
B $8 {log}_{e} 2 - \frac{7}{3}$
C $16 {log}_{e} 2 - 6$
D $16 {log}_{e} 2 - \frac{14}{3}$