Find the area of the region {(x,y):x2≤y≤|x|}.
Video Solution
Text Solution
Consider the equations
x2=y
and y|x|
Clearly x2=y represents an upward parabola with its vertx at O(0,0).All the points inside the parabola represent x2≤y
Also y=|x|={xwhen x ≥0−x when x <0
Thus , the shaded portion is the required region.
In each of the given equation , the equation remains unchanded when x is replaced by -x .
So, each of the given curves is symmetricaol about the y-axies.
∵ required area =2(area OEAO).
x2=y
and y=x
Using (iv) in (iii) ,we get x2=x⇒x(x−1)=0⇒x=0orx=1
Now (x=0⇒y=0)and(x=1⇒y=1)
Thus , the line y=x and the curve x2=y intersect O(0,0) and A(1,1).Draw AD⊥OXandBC⊥OX
∴ required area
=2(area OEAO)=2[area ODAO)-(area ODAEO)]
=2 [(area between y=x and the x-axis form x=0 to x=1)-(area between x^2 =y and the x-axis from x =0 to x =1 )
=21∫0 y dx for the line OA-1∫0y dx for the curve OEA⎫⎪⎬⎪⎭
2⎡⎢⎣1∫0xdx−1∫0x2dx⎤⎥⎦=2{[x22]10−[x33]10}=2[12−13]
=(2×16)=13 sq unit
Hence , the required aera is 13 sq units
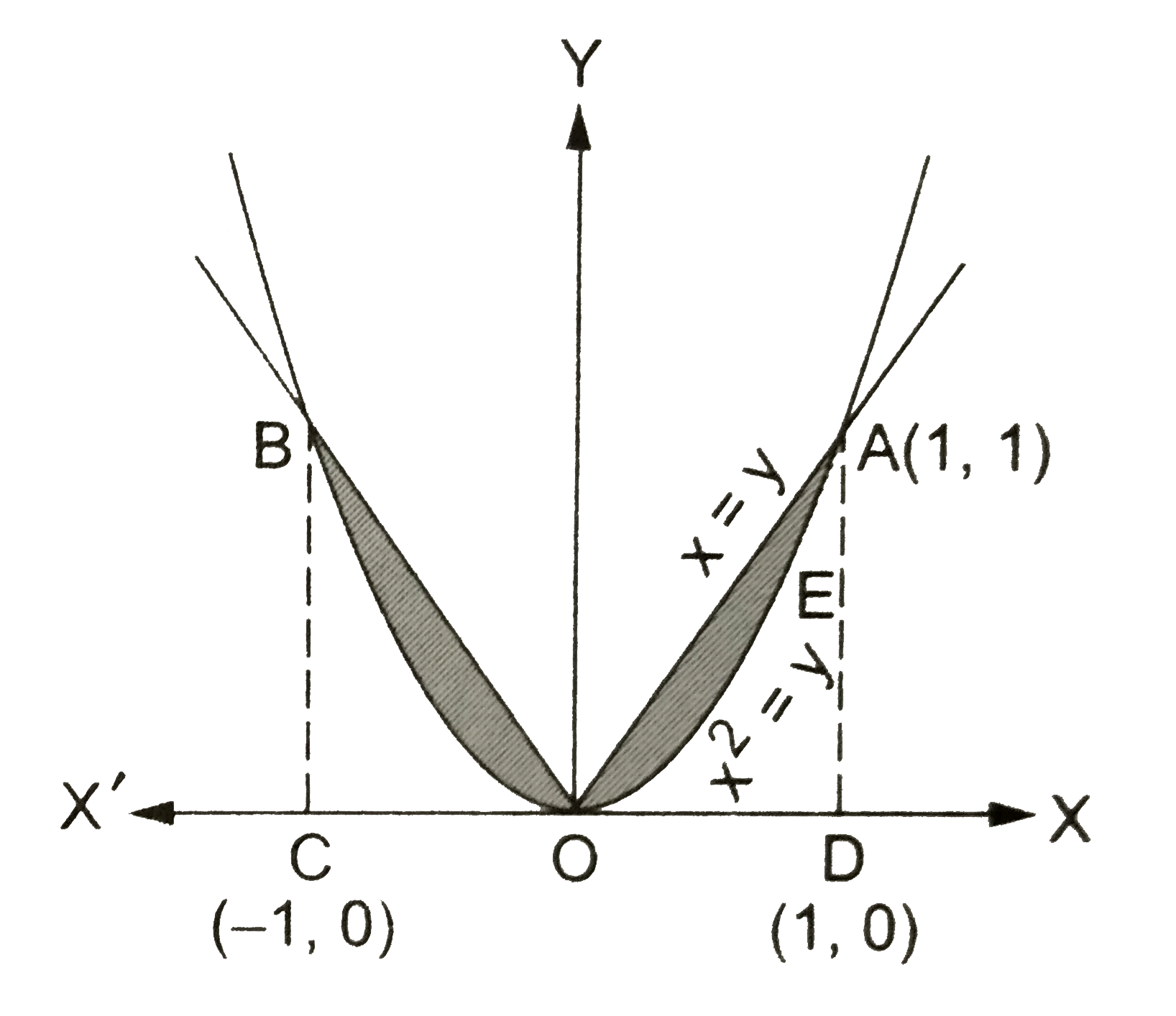
|
Topper's Solved these Questions
- AREA OF BOUNDED REGIONS BOOK - RS AGGARWALCHAPTER - AREA OF BOUNDED REGIONS EXERCISE - Exercise 17
39 Videos
- APPLICATIONS OF DERIVATIVESBOOK - RS AGGARWALCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Objective Questions
89 Videos
- BAYES'S THEOREM AND ITS APPLICATIONSBOOK - RS AGGARWALCHAPTER - BAYES'S THEOREM AND ITS APPLICATIONSEXERCISE - Exercise 30
18 Videos
Similar Questions
Knowledge Check
The area of the region {(x,y):xy≤8,≤y≤x2} is
A8loge2−143B8loge2−73C16loge2−143D16loge2−6The area of region{(x,y):x2+y2≤1≤x++y} is
Aπ25sq unitsBπ22sq unitsCπ24sq unitsD(π4−12) sq units
Find the area of the region:
(i) {(x,y):x2≤y≤x}
(ii) {(x,y):x2≤y≤|x|}.
View SolutionFind the area of the region [x,y):x2+y2≤1≤x+y}
View SolutionFind the area of the region {(x,y):0≤y≤x2+1,0≤y≤x+1,0≤x≤2}.
View SolutionFind the area of the region {(x,y):x2+y2≤1≤x+y}
View SolutionFind the area of the region {(x,y):x2+y2≤2ax , y2≤ax , x≤0 , y≤0}
View SolutionDraw the rough sketch and find the area of the region:
{(x,y):4x2+y2≤4,2x+y≥2}
View Solution
