Find the area of the shaded region in figure.

Video Solution
Text Solution
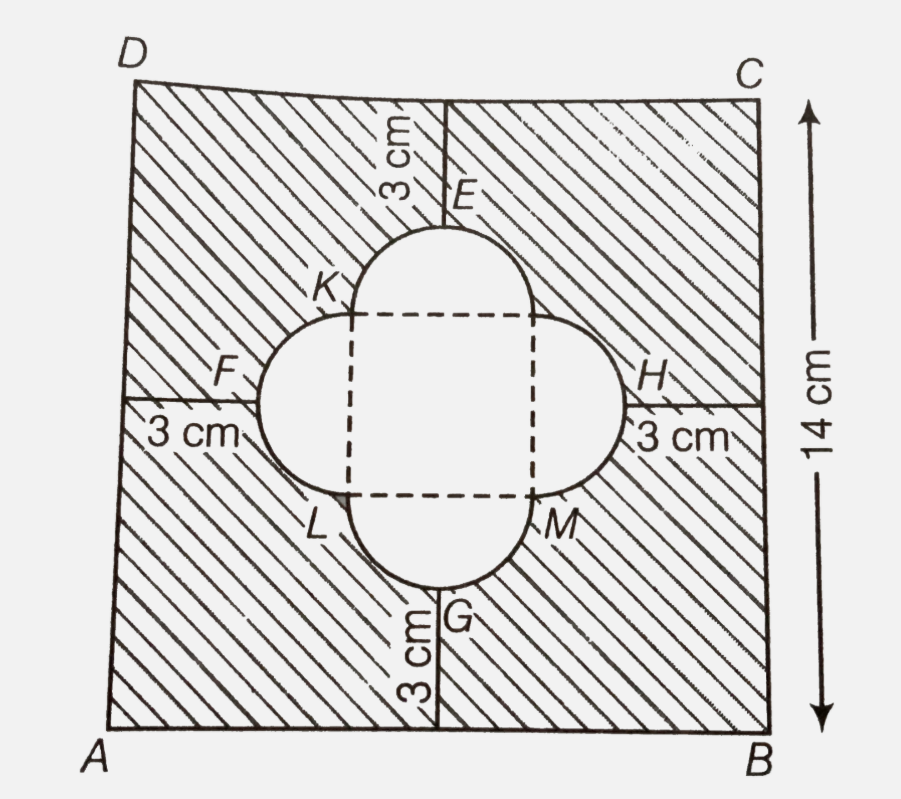
Join GH and FE
Here, breadth of the rectangle BC = 12m
∴ Breadth of the inner rectangle EFGH = 12−(4+4)=4cm
which is equal to the diameter of the semi-circle EJF, d = 4m
∴ Radius of semi-circle EJF , r= 2m
∴ Length of inner rectangle EFGH = 26−(5+5)=16m
∴ Area of two semi-circles EJF and HIG = 2(πr22)=2×π(2)22=4πm
Now, area of inner rectangle EFGH = EH×FG=16×4=64m2
and area of outer rectangle ABCD = 26×12=312m2
∴ Area of shaded region = Area of outer rectangle - (Area of two semi - circles + Area of inner rectangle)
= 312−(64+4π)=(248=4π)m2

|
Topper's Solved these Questions
Similar Questions
Knowledge Check
In the adjoining figure, ABCD is a square of side 7 cm and two semicircles are drawn inside of it with AB and CD as diameters. Find the area of the shaded region (in cm2).
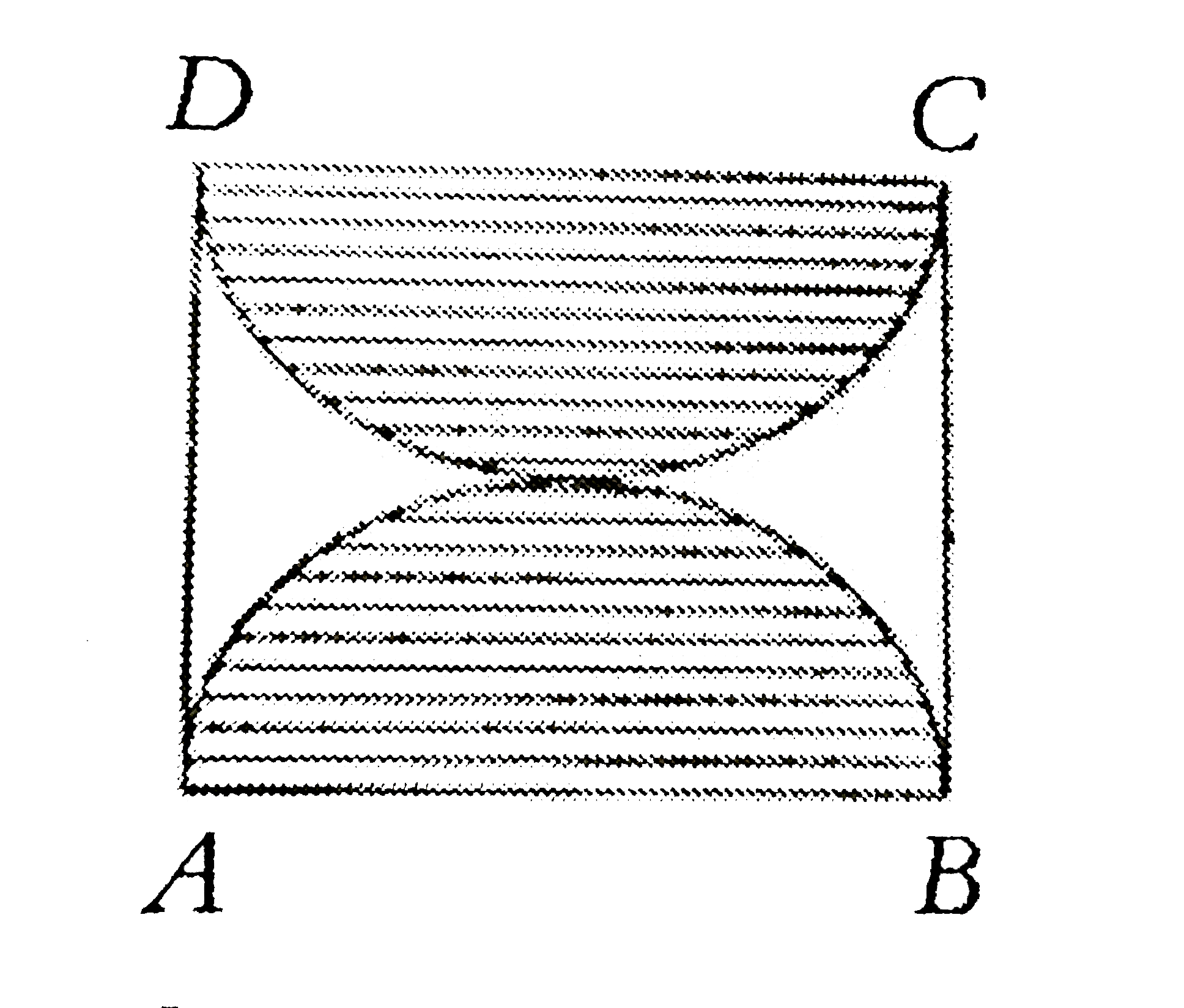 A144 m2B164 m2C184 m2D154 m2
A144 m2B164 m2C184 m2D154 m2
In the figure given below, PQRS is a square of side 14 cm and two semicircles are drawn inside of it with PQ and SR as diameters. Find the area of the shaded region in the figure.

View SolutionFind the area of the shaded region in the figure given below where radii of the two concentric circles with centre O are 7 cm and 14 cm respectively and ∠AOC=40∘.

View Solution21. Find the area of the shaded region i
View SolutionFind the area of the shaded region of the figure given below.
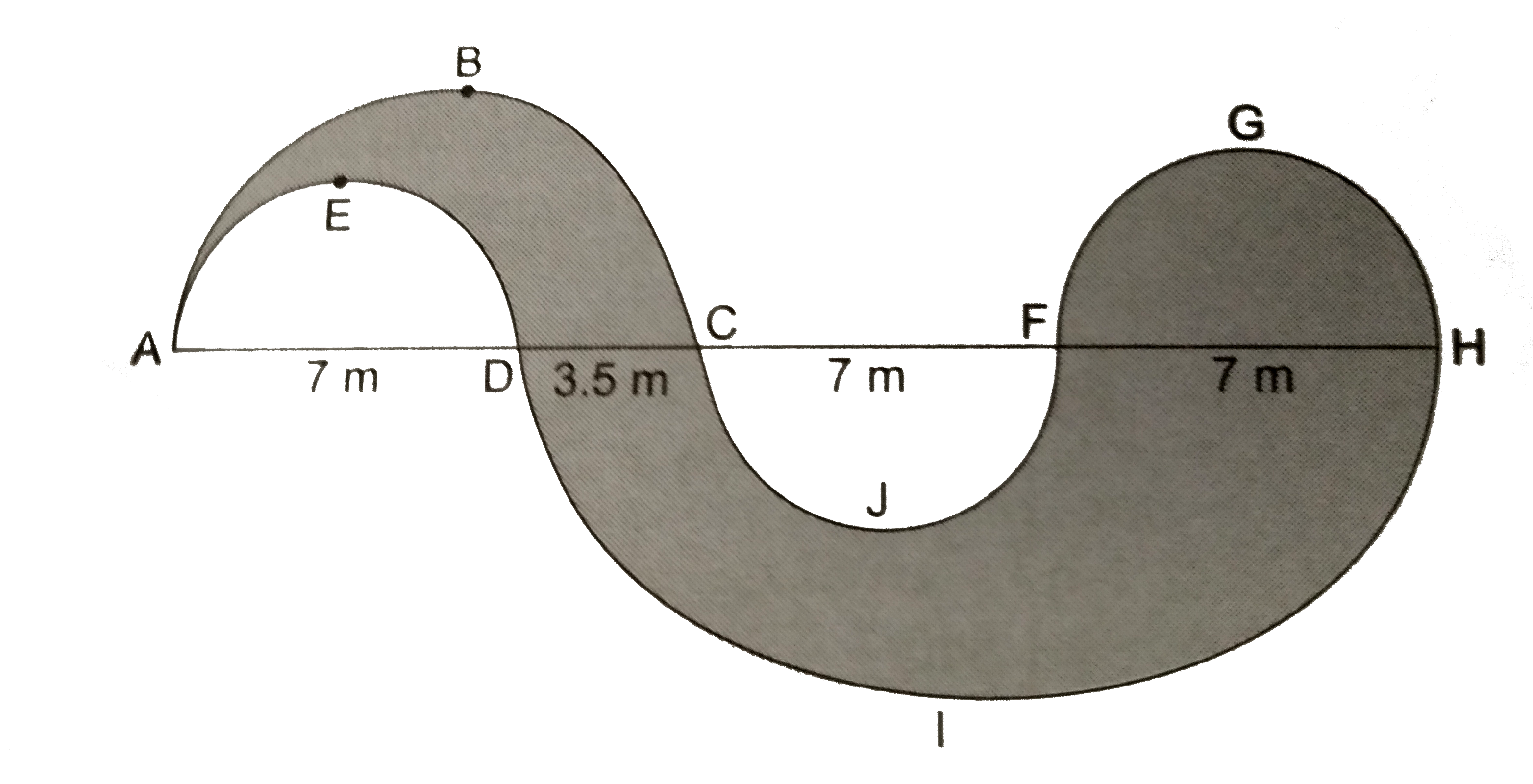
View SolutionFind the area of the shaded region given in figure
View SolutionFind the area of the shaded region given in figure.
View SolutionFind the area of the shaded region in given figure if ABCD is a rectangle with sides 8 cm and 6 cm and O is centre of circle. [Take π=3.14]
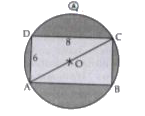
View Solution


