Find the area of the triangle formed by the lines joining the vertex of the parabola x2=12y to the ends of its latus rectum.
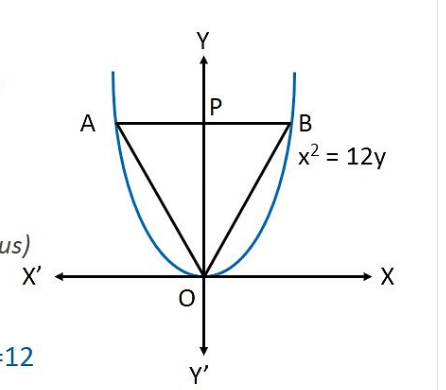
The given parabola ia x2=12y
on comparing this equation with x2=4ay, we get
⇒4a=12
=>a=3
So, the coordinates of focus is s(0,a)=s(0,3)
Let AB be the latus rectum of the given parabola
coordinates of end point of latus rectum are (−2a,a),(2a,a)
coordinates of A are (−6,3) while the coordinates of B are (6,3)
∴ the vertices of △OAB
=12|x1(y2−y3)+x2(y3−y2)+x3(y1−y2)|
=12|0(3−3)+(−6)(3−0)+6(0−3)|
=12|(−6)(3)+6(−3)|
=12|(−18−18)|
=12|−36|
=12×36
=18sq units
Topper's Solved these Questions
- CONIC SECTIONSBOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.1
15 Videos
- CONIC SECTIONSBOOK - NCERTCHAPTER - CONIC SECTIONSEXERCISE - EXERCISE 11.2
12 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - NCERTCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - EXERCISE 5.4
6 Videos
- INTRODUCTION TO THREE DIMENSIONAL GEOMETRYBOOK - NCERTCHAPTER - INTRODUCTION TO THREE DIMENSIONAL GEOMETRYEXERCISE - EXERCISE 12.1
4 Videos
Similar Questions
Knowledge Check
The area of the triangle formed by the lines joining the focus of the parabola y2=12x to the points on it which have abscissa 12 are
A100 sq. unitsB130 sq. unitsC120 sq. unitsD108 sq. units
Find the area of the triangle formed by the lines joining the vertex of the parabola x2=8y to the ends of its latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola x2=−36y to the ends of the latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of he parabola x2=12y to the ends of its latus-rectum.
View SolutionFind the area of the triangle formed by the lines joining the vertex of the parabola y2=16x to the ends of the latus rectum.
View SolutionFind the area of the triangle formed by the lines joining the focus of the parabola y2=4x to the points on it which have abscissa equal to 16.
View SolutionFind the area of the triangle formed by the vertex and the ends of the latus rectum of the parabola
x2=−36y.
View SolutionFind the equation of a line joining the vertex of parabola y2=8x to its upper end of latus rectum.
View Solution