Find the co-ordinates of a point which divide the segment AB in ratio 1:4 internally , where A (7,−8)andB(−4,3) .
To find the coordinates of a point C that divides the line segment AB in the ratio 1:4 internally, we will use the section formula. The coordinates of points A and B are given as A(7,−8) and B(−4,3).
1. Identify the coordinates of points A and B:
- A(7,−8)
- B(−4,3)
2. Use the section formula:
The section formula for a point C(x,y) that divides the line segment AB in the ratio m:n is given by:
C(mx2+nx1m+n,my2+ny1m+n)
where (x1,y1) are the coordinates of point A and (x2,y2) are the coordinates of point B.
3. Substitute the values:
Here, m=1, n=4, x1=7, y1=−8, x2=−4, and y2=3.
- For the x-coordinate:
x=1⋅(−4)+4⋅71+4=−4+285=245
- For the y-coordinate:
y=1⋅3+4⋅(−8)1+4=3−325=−295
4. Combine the results:
Thus, the coordinates of point C are:
C(245,−295)
Final Answer:
The coordinates of the point C that divides the segment AB in the ratio 1:4 internally are:
C(245,−295)
- A(7,−8)
- B(−4,3)
The section formula for a point C(x,y) that divides the line segment AB in the ratio m:n is given by:
C(mx2+nx1m+n,my2+ny1m+n)
where (x1,y1) are the coordinates of point A and (x2,y2) are the coordinates of point B.
Here, m=1, n=4, x1=7, y1=−8, x2=−4, and y2=3.
x=1⋅(−4)+4⋅71+4=−4+285=245
y=1⋅3+4⋅(−8)1+4=3−325=−295
Thus, the coordinates of point C are:
C(245,−295)
The coordinates of the point C that divides the segment AB in the ratio 1:4 internally are:
C(245,−295)
Topper's Solved these Questions
- BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Very Short Answer type Questions )17videos
DIKSHA QUESTIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -IV: Geometry (Triangles) (Long Answer Type Questions)4videos
DIKSHA QUESTIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - DIKSHA QUESTIONS EXERCISE - Unit -III: Coordinate Geometry (Coordinate Geometry ) (Long Answer Type Questions )11videos
DIKSHA QUESTIONS
- BOOK - OSWAL PUBLICATIONCHAPTER - COORDINATE GEOMETRYEXERCISE - SELF ASSESSMENT20videos
COORDINATE GEOMETRY
- BOOK - OSWAL PUBLICATIONCHAPTER - INTRODUCTION TO TRIGONOMETRY EXERCISE - Self - Assessment15videos
INTRODUCTION TO TRIGONOMETRY
Similar Questions
(i) Find the co-ordinates of a point which divides the line segment joining the points A(2,-1,3) and B(4,3,1) in the ratio 3 : 4 externally.
(ii) The 'x' co-ordinate of a point on line segment joining the points (2, -3, 4) and (8, 0, 10) is 4. Find the co-ordinate of this point.View SolutionFind the coordinates of the point which divides the line segment joining (−1, 3) and (4, −7) internally in the ratio 3:4 .
View SolutionFind the corrdinates of the point which divides the line segment joining the points A(2,-6,8) and B (-1,3,-4) externally in the ratio 1:3.
View SolutionFind the co-ordinate of point A which divides segment PQ in the ratio a:b
P(−3,7),Q(1,−4),a:b=2:1View SolutionFind the co - ordinates of the point which divides the join (1,7)and(4,−3) in the ratio 2:3.
View Solution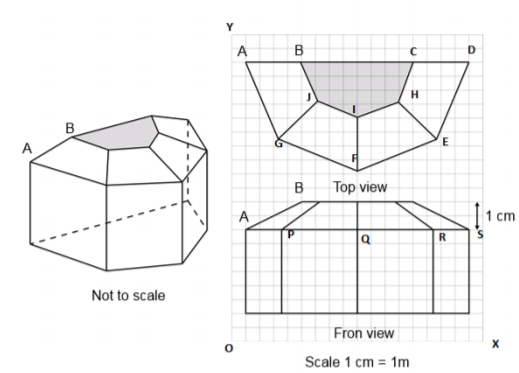
Refer to Front View Find the co-ordinates of the point which divides the line segment joining the points A and B in the ratio 1:3 internally. (i) (9.5,2.0) (ii) (2.0,9.5) (iii) (3.0,7.5) (iv) (2.0,8.5)View SolutionIf A(3,1,−2)andB(1,−3,−1) be two points find the coordinates coordinates of the point which divides the line segment AB. Internally in the ratio 1:3
View SolutionIn each of the following examples find the co-ordinates of point A which divides segment PQ in the ratio a:b .
P(2,6),Q(-4,1) ,a:b=3:4View SolutionFind the co-ordinates of the point which divides the line segment joining the points (2,3,-4) and (4,-1,2) in the ratio (i) 2 : 3 internally, (ii) 4 : 3 externally.
View SolutionFind the co-ordinates of a point which divides the line segment joining the points (5, 1) and (-10, 11) in the ratio 2 : 3 internally.
View Solution

