Doubtnut Promotions Sticky

Find the co-ordinates of circumcentre and radius of circumcircle of △ ABC if A(7,1) ,B(3,5) and C(2,0) are given .

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

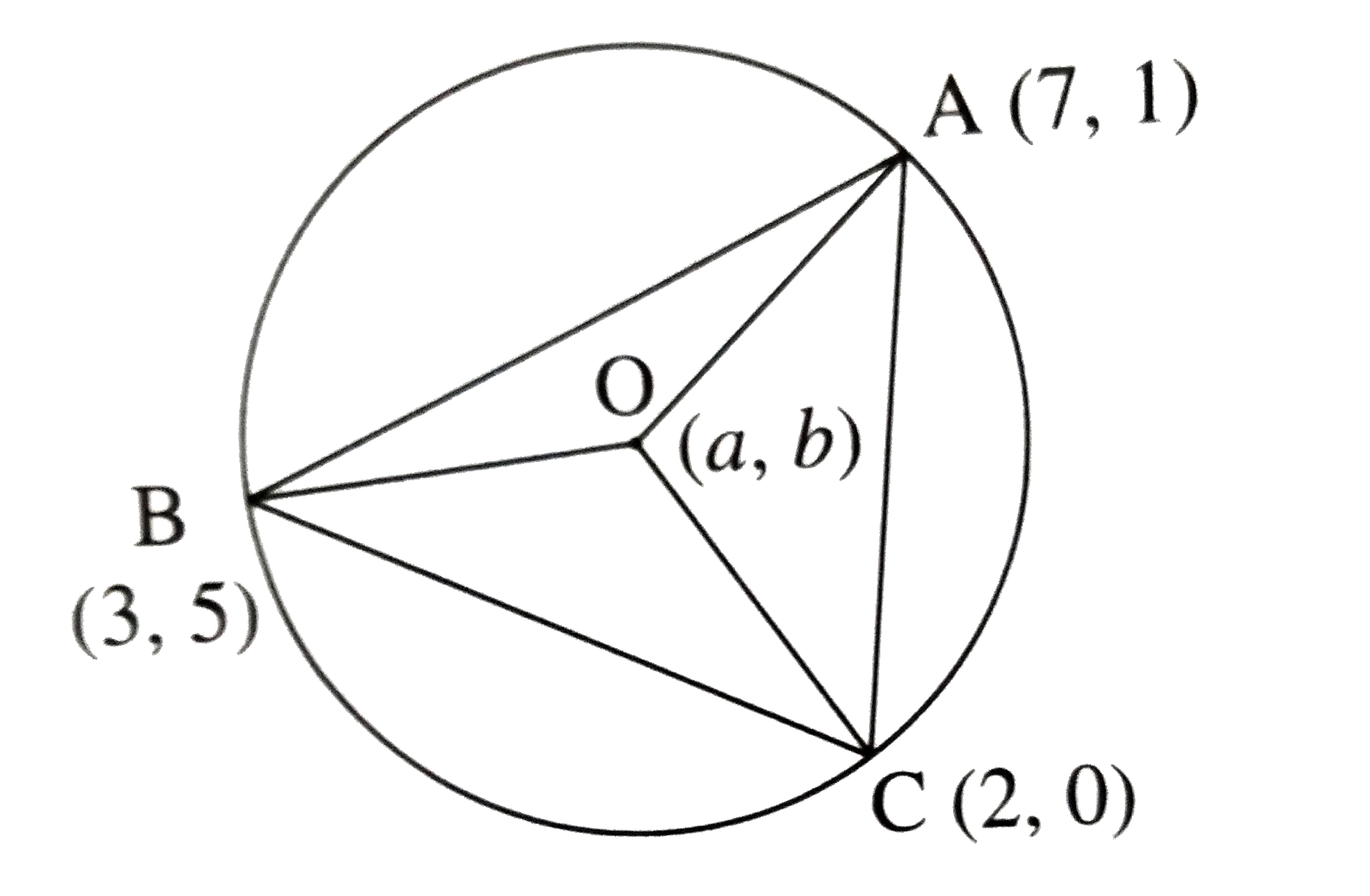
ocr_image
A(7,1),B(3,5) and C(2,0)
Let O(a,b) be the circumcentre.
OA−OB ………..(Radii of the same circle)
∴√(a−7)2+(b−1)2=√(a−3)2+(b−5)2
………….(Distance formula)
Squaring both the sides we get
(a−7)2+(b−1)2=(a−3)2+(b−5)2
∴a2−14a+49+b2−2b+1
=a2−6a+9+b2−10b+25
∴−14a−2b+50=−6a−10b+34
∴−14a+6a−2b+10b=34+50
∴−8a+8b=−16
−8(a−b)=−16
∴a−b=−16−8
∴a−b=2.....1
OB=OC .........(Radii of the same circle)
∴√(a−3)2+(b−5)2=√(a−2)2+(b−0)2
Squaring both the sides we get,
(a−3)2+(b−5)2=(a−2)2+(b−10)2
∴a2−6a+9+b2−10b+25=a2−4a+4+b2
∴−6a−10b+34=−4a+4
∴−6a+4a−10b=−4−34
∴−2a−10b=−30
∴−2a−10b=−30
∴a=6b=−30−2
∴a+5b=15............2
Subtracting 1 from 2 we get
ocr_image
∴b=136
Substituting b=136 in 1 we get
a−b=2
∴a−136=2
∴a=2+136
∴a=12+136
∴a=256
∴ coordinates of circumcentre are (256,136)
By distance formula,
Radius =OC=√(2−256)2+(0−136)2
=√(12−256)2+(−136)2
=√(−136)2+(−136)2
=√16936+16936
=√169×236
=13√26
Radius of the circumcircle is 13√26
Coordinates of circumcentre are (256,136)
and radius of circumference is 13√26.

|