Find the cube of (2a−3b)Solution in Punjabi
The correct Answer is:(i) mεg(−∞,7−√32) (ii) mε(7+√332,∞) (iii) mεϕ
(iv) mε(7−√32,11−√732)∪(7+√332,11+√732)
(v) mε(0,3) (vi) mε(7−√32,7+√332)
(vii) mε(7−√332,11−√732)∪(7+√332,11+√732)
(viii) mε(7−√32,7+√332)∪(7+√32,∞)
(ix) mε(−∞,7−√332)∪((7−√332,7+√332)
(x) mε((11-sqrt(73))/2,(7+sqrt(3))/2)
∵2x2−2(2m+1)x+m(m+1)=0[∵mεR]
∴D=[−2(2m+1)]2−8m(m+1)[D=b2−4ac]
=4{(2m+1)2−2m(m+1)}
=4(2m2+2m+1)
=8(m2+m+12)=8{(m+12)2+14}>0
or D>0,∀mεolonR……i
x coordinate of vertex =−b2a=2(m+1)4=(m+12).....ii
and let
f(x)=x2−(2m+1)x+12m(m+1) ...........iii
(i) Both roots are smaller than 2.

Consider the following cases:
Case I D≥0
∴mεR [from Eq. (i) ]
CaseII x-coordinate of vertex <2.
⇒m+12<0 [from Eq. (ii) ]
or m<32
Case III f(2)>0
⇒4−(2m+1)2+12m(m+1)>0
⇒m2−7m+4>0
∴mε(−∞,7−√32)∪(7+√332,∞)
Combining all cases we get
mε(−∞,7−√32)
(ii) Both roots are greater than 2.
Consider the following cases.
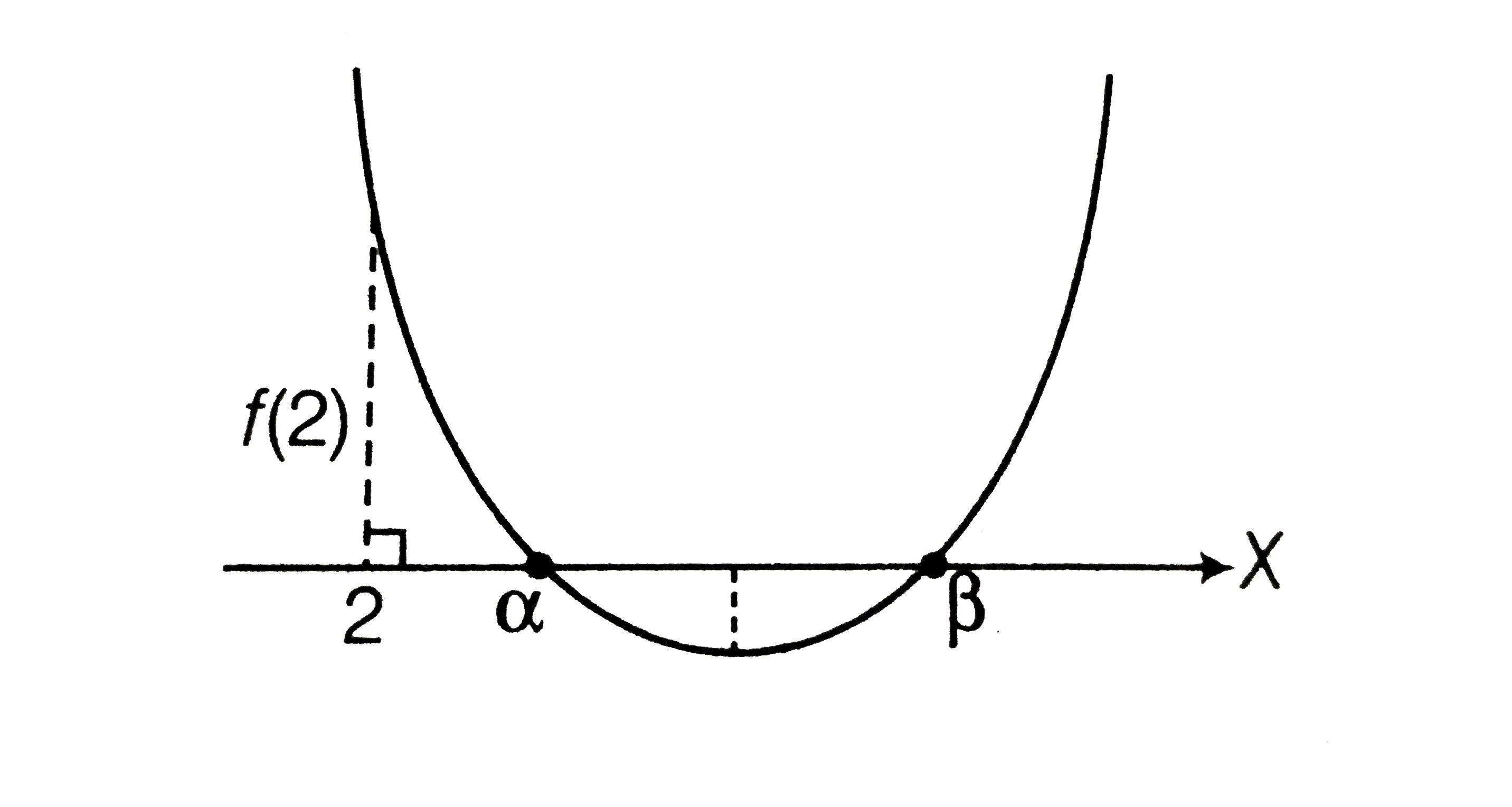
Case I D≥0
∴mεR[from Eq. (i)]
Case II x- coordinate of vertex >2
⇒m+12>2[ from Eq. (ii)]
∴m>32
Case III f(2)>0
mε(−∞,7−√332)∪(7+√332,∞) [from part (a) ]
Combining all cases, we get
mε(7+√332,∞)
(iii) Both roots lie in the interval (2,3).
Consider the following cases:

CAse I D≥0
∴mεR [from Eq. (i)]
Case II f(2)>0
∴mε(−∞,7−√32)∪(7+√332,∞) [from part (a)]
Case Case III f(3)>0
⇒9−3(2m+1)+12m(m+1)>0
or m2−11m+12>0
:mε(−∞,11−√732)∪(11+√732,∞)
Case IV 2<x -coordinate of vertex <3
⇒2<m+12<3
or 32<m<52 or mε(32,52)
Combining allcases we get
mεϕ
(iv) Exactly one root lie in the interval (2,3).
Consiser the following cases:
Case I D>0
∴mεR [from Eq (i) ]
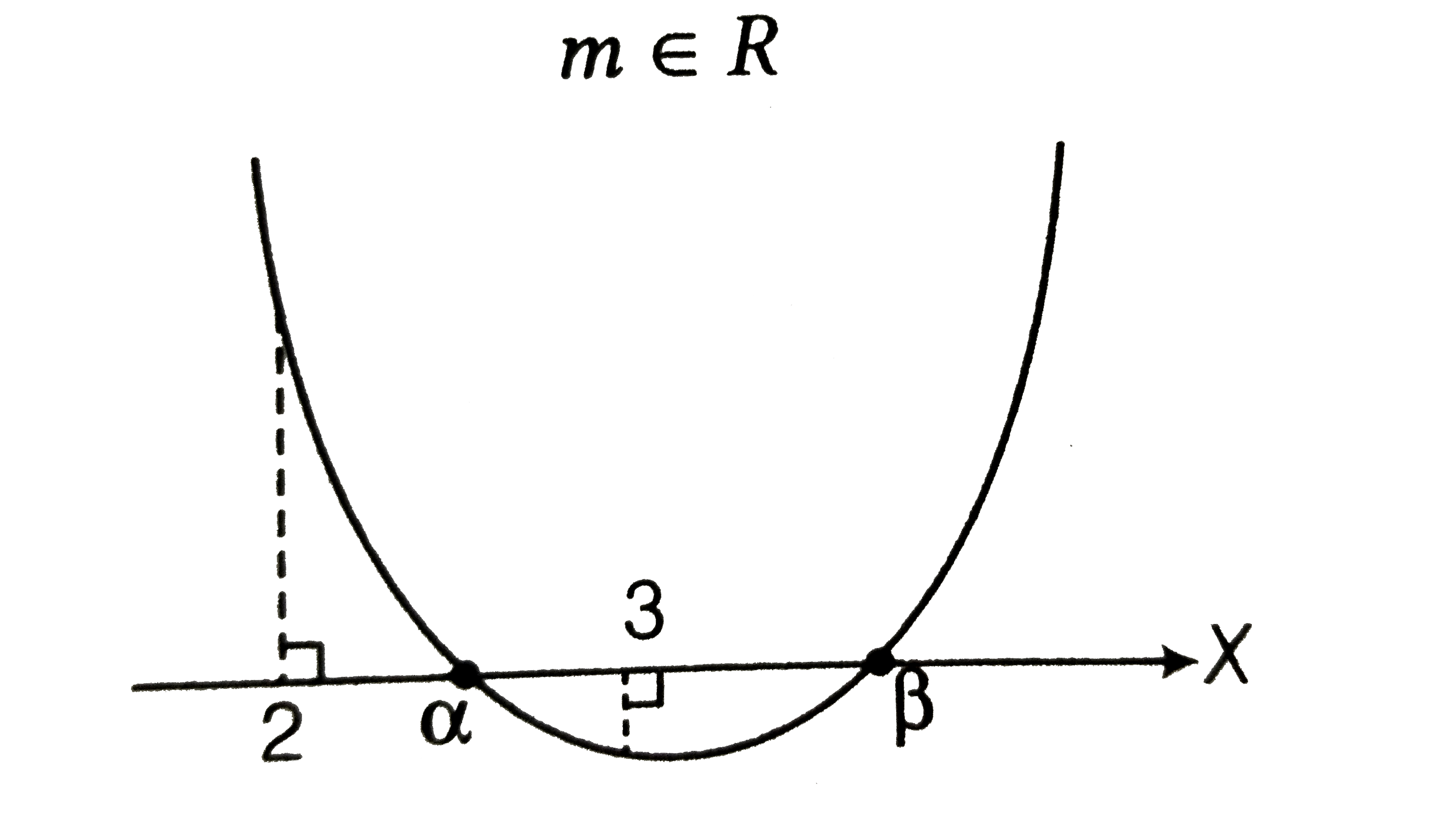
Case II f(2)f(3)<0
(4−2(2m+1)+12m(m+1))
(9−3(2m+1)+12m(m+1))<0
⇒(m2−7m+4)(m2−11m+12)<0
⇒(m−7−√332)(m−7+√332)
(m−11−√732)(m−11+√732)<0
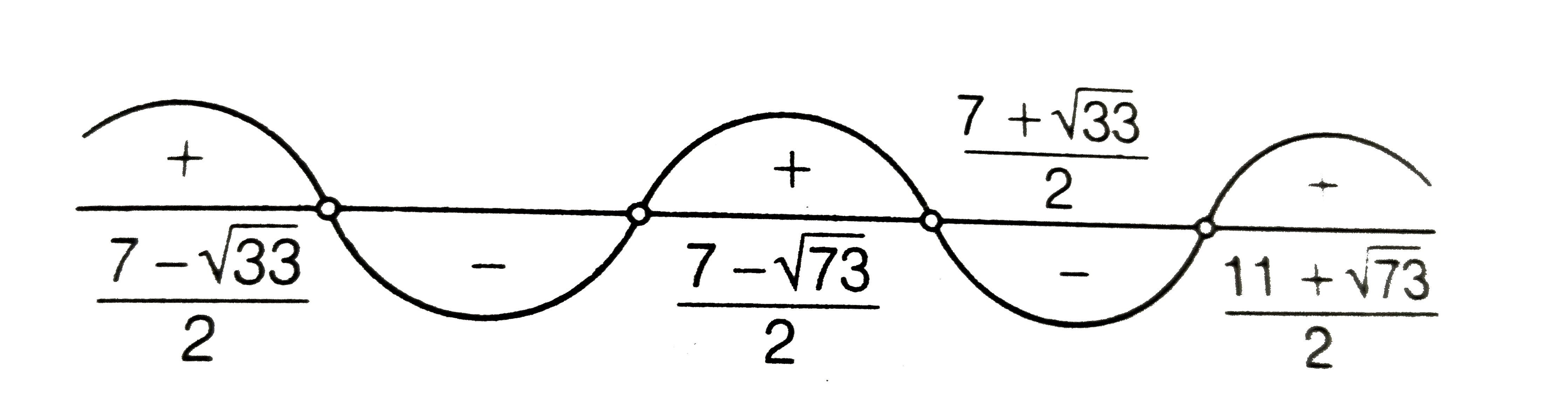
∴mε(7−√332,11−√332)∪(7+√332,11+√732)
Combining all cases we get
mε((7-sqrt(33))/2,(11-sqrt(73))/2))uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(v)O≠i√ssmal≤rthan1andtheotheri√sgreaterthan1.<br>Consiserthefollow∈gcases.<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S06.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:.m epsilonR[omEq.(i)]<br>CaseIIf(1)lt0<br>implies1-(2+1)+1/2m(m+1)lt0[omEq.(iii)]<br>impliesm^(2)-3mlt0<br>impliesm(m-3)lt0<br>:.m epsilon (0,3)<br>Comb∈∈g⊥hcaseswe≥t<br> m epsilon(0,3)<br>(vi)O≠i√sgreaterthan3andtheotheri√ssmal≤rthan2.<bR>Consiserthefollow∈gcases<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S07.pngwh=80%mx-autosty≤=background:white;><br>CaseIDgt0<br>:. m epsion R[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-8m+4lt0<br>:.(7-sqrt(33))/2ltmlt(7+sqrt(33))/2<br>:. m epsilon ((7-sqrt(33))/2ltm lt (7+sqrt(33))/2<br>:. M epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.(11-sqrt(73))/2ltmlt (11+sqrt(73))/2<br>:. m epsilon ((11-sqrt(73))/2, (11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((7-sqrt(33))/2, (7+sqrt(33))/2)<br>(vii)At≤∗o≠l√ies∈the∫erval(2,3).<br>i.e.(d)uu(c)<br>:.mepsilon((7-sqrt(33))/2,(11-sqrt(73))/2)uu((7+sqrt(33))/2,(11+sqrt(73))/2)<br>(viii)At≤∗o≠i√sgreaterthan2.<br>i.e(Exactlyo≠i√sgreaterthan2)uu(Boths√aregreater2).<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S08.pngwh=80%mx-autosty≤=background:white;><br>of(Exactlyo≠i√sgreaterthan2)uu(b)…..i<br>Consrthefollow∈gcases:<br>CaseIDgt0<br>:. m epsilon[omEq.(i)]<br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:.m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>Comb∈∈g⊥hcaseswe≥t<br>m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)………ii<br>F∈allyomEqsiandiiwe≥t<br> m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)uu((7+sqrt(33))/2,oo)<br>(ix)At≤∗o≠i√ssmal≤rthan2.<br>i.e(Exactlyo≠i√ssmal≤rthen2)uu(Boths√aresmal≤rthan2)<br>or(h)IIuu(a)<br>We≥tm epsilon (-oo,(7-sqrt(33))/2)uu((7-sqrt(33))/2,(7+sqrt(33))/2)<br>(x)Both2and3liebetweenalphaandbeta<br>Consrthefollow∈gcases:<br>CaseDgt0<br>:. mepsilonR[omEq(i)]<br><imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/ARH_SKG_ALG_C02_E12_002_S09.pngwh=80%mx-autosty≤=background:white;><br>CaseIIf(2)lt0<br>impliesm^(2)-7m+4lt0<br>:. m epsilon ((7-sqrt(33))/2,(7+sqrt(33))/2)<br>CaseIIIf(3)lt0<br>impliesm^(2)-11m+12lt0<br>:.m epsilon((11-sqrt(73))/2,(11+sqrt(73))/2)<br>Comb∈∈gallcaseswe≥t<br>m epsilon ((11-sqrt(73))/2,(7+sqrt(33))/2)
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
35 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise (Statement I And Ii Type Questions)
7 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
In the quadratic equation ax2+bx+c=0. if δ=b2−4ac and α+β,α2+β2,α3+β3 are in G.P. and α,β are the roots of ax2+bx+c=0
View SolutionStatement -1 If the equation (4p−3)x2+(4q−3)x+r=0 is satisfied by x=a,x=b nad x=c (where a,b,c are distinct) then p=q=34 and r=0
Statement -2 If the quadratic equation ax2+bx+c=0 has three distinct roots, then a, b and c are must be zero.
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View Solutionनिम्नलिखित प्रत्येक व्यंजक के गुणनखण्ड़ कीजिए:
(2a+3b)2+2(2a+3b)(2a−3b)+(2a−3b)2
View SolutionIf 2a−3b2a+3b=13, then find the value of 2a3−3b32a3+3b3.
View Solutionಕೆಳಗಿನ ಘನಗಳನ್ನು ವಿಸ್ತ್ರತ ರೂಪದಲ್ಲಿ ಬರೆಯಿರಿ : (2a−3b)3
View Solutionకింది ఘనలను విస్తరించండి. (2a+3b)3
View SolutionWrite the following cube in expanded : (2a−3b)3.
View Solution2a-3b,2a+3b का माध्य ज्ञात करें।
View SolutionIf A=[023214]
andB=[763145]
find 2A+3B,2A−3B.
View Solutionसरल कीजिए -
(2 a - 3b) (2a + 3b)
View Solutionਹੇਠ ਲਿਖੇ ਘਣ ਨੂੰ ਵਿਸਤ੍ਰਿਤ ਰੂਪ ਵਿੱਚ ਲਿਖੋ:- (2a−3b)3
View SolutionEvaluate: (2a−3b)2
View SolutionEvaluate: (2a+3b)3
View SolutionFind the cube of: 5a+3b
View Solution
