Find the dimensions of the rectangle of perimeter 36cm which will sweep out a volume as large as possible when revolved about one of its sides.
Video Solution
Text Solution
Let breadth and length of the rectangle be x and y, respectively.

∴ Perimeter of the reactangle = 36 cm
⇒2x+2y=36
⇒x+y=18
⇒y=18−x …………….(i)
Let the rectangle is being revolved about its length y.
Then, volume (V) of resultant cylinder =πx2.y
⇒V=πx2.(18−x) [∴V=πr2h] [using Eq. (i)]
=18πx2−πx2=π[18x2−x3]
On differentiating both sides w.r.t. x, we get
dVdx=π(36π−3x2)
Now, dVdx=π(36π−3x2)
Now, (dV)(dx)=0
⇒36x=3x2
⇒3x2−36x=0
⇒3(x2−12x)=0
⇒3x(x−12)=0
∴x=12 [∴,x≠0]
Again, differentiating w.r.t. x, we get
d2Vdx2=π(36−6x)
⇒d2V(dx2)x=12=π(36−6×12)=−36π<0
At x=12, volume of the resultant cylinder is the maximum.
So, the dimension of rectangle are 12 cm and 6 cm, respectively.
∴ Maximum volume of resultant cylinder.
(V)x=12=π[18.(12)2−(12)3]
=π[122(18−12)]
=π×144×6
=864πcm3
|
Updated on:21/07/2023
Topper's Solved these Questions
Similar Questions
Knowledge Check
- Question 1 - Select One
Find the dimensions of the rectangle of perimeter 36cm which will sweep out a volume as large as possible when revolved about one of its sides.
A10,8B11,7C12,6DNone - Question 2 - Select One
The locus of a rectangle, when the rectangle is rotated about one of its sides is a ______
AplineBsphereCconeDcylinder - Question 3 - Select One
Find the perimeter of a square, each of whose sides measures 3.6 cm.
A=14.4cmB=24.4cmC=34.4cmD=12.4cm
Find the breadth of the rectangle if its length is 70 cm and perimeter is 200 cm
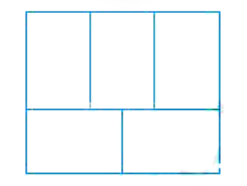
View SolutionIn Fig. 9.44 a rectangle with perimeter 264 cm is divided into five congruent rectangles. Find the perimeter of one of the rectangles.
 View Solution
View Solutionadjcent sides of a rectangle are 3.6cm and 1.5cm .Find the length of the diagonal
View Solution(3) The ratio of length of breadth of rectangle is 3:1 and its perimeter is 36cm Find the length , breadth of the rectangle.
View SolutionThe sides of a triangle are in the ratio 1:2:3. If the perimeter is 36 cm, find its sides.
View Solution

