Find the distance of the point $(2, 3, 4)$ from the line $\frac{x + 3}{3} = \frac{y - 2}{6} = \frac{z}{2}$ measured parallel to the plane $3 x + 2 y + 2 z - 5 = 0$ .

Video Solution

Text Solution

Verified by Experts

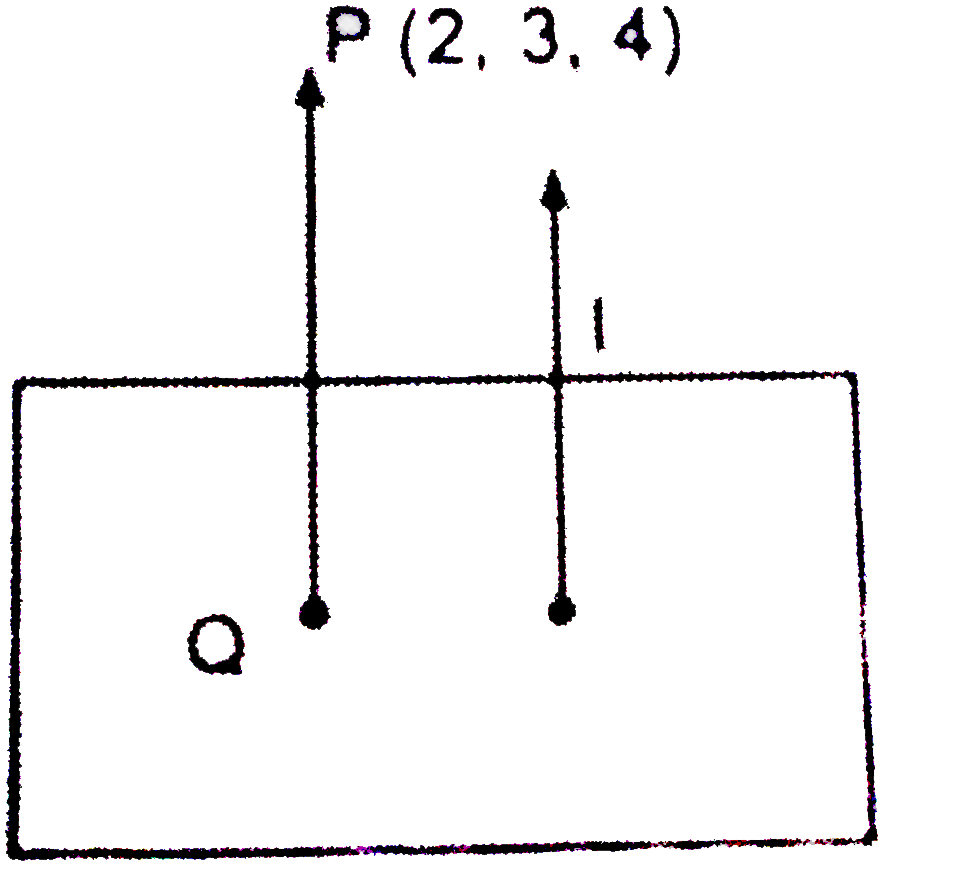
Let l be the given below
$l : \frac{x + 3}{3} = \frac{y - 2}{6} = \frac{z}{2}$ and the given point be $P (2, 3, 4)$ . Let the given point be $P (2, 3, 4)$ Let a line parallel to line 'l' through P meets the plane at Q.
Equation of line PQ
$\frac{x - 2}{3} = \frac{y - 3}{6} = \frac{z - 4}{2} = λ$ (say)
Co-ordinates of point Q lies on PQ are
$(3 λ + 2, 6 λ + 3, 2 λ + 4)$
Point Q lies on the plane $3 x + 2 y + 2 z + 5 = 0$
$∴ 3 (3 λ + 2) + 2 (6 λ + 3) + 2 (2 λ + 4) + 5 = 0$
$\Rightarrow 9 λ + 6 + 12 λ + 6 + 4 λ + 8 + 5 = 0$
$\Rightarrow 45 λ + 25 = 0$
$\Rightarrow λ = - 1$
$∴$ Co-ordinates of $Q = (- 1, - 3, 2)$
and $P Q = \sqrt{{(2 + 1)}^{2} + {(3 + 3)}^{2} + {(4 - 2)}^{2}}$
$= \sqrt{9 + 36 + 4} = 7$ units.

The distance of the point (3,8,2) from the line $\frac{x - 1}{2} = \frac{y - 3}{4} = \frac{z - 2}{3}$ measured parallel to the plane $3 x + 2 y - 2 z = 0$ is
A2
B3
C6
D7
Distance of point $P (- 2, 3, 4)$ from the line $\frac{x + 2}{3} = \frac{2 y + 3}{4} = \frac{3 z + 4}{5}$ measured parallel to the plane $8 x + 6 y - 9 z + 1 = 0$ is
A $\frac{\sqrt{301}}{2}$
B $\frac{\sqrt{401}}{2}$
C $\frac{\sqrt{307}}{2}$
D $\frac{\sqrt{207}}{2}$
The distance of the point (-2,4,-5) from the line $\frac{x + 3}{3} = \frac{y - 4}{5} = \frac{z + 8}{6}$ is
A $\frac{\sqrt{37}}{10}$
B $\sqrt{\frac{37}{10}}$
C $\frac{37}{\sqrt{10}}$
D $\frac{37}{10}$