Find the equation of the chord of the circle $x^{2} + y^{2} = a^{2}$ passing through the point (2, 3) farthest from the center.

A

$2 x + 3 y = 13$

B

$3 x - y = 3$

C

$- 2 y + 4 = 0$

D

$x - y + 1 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

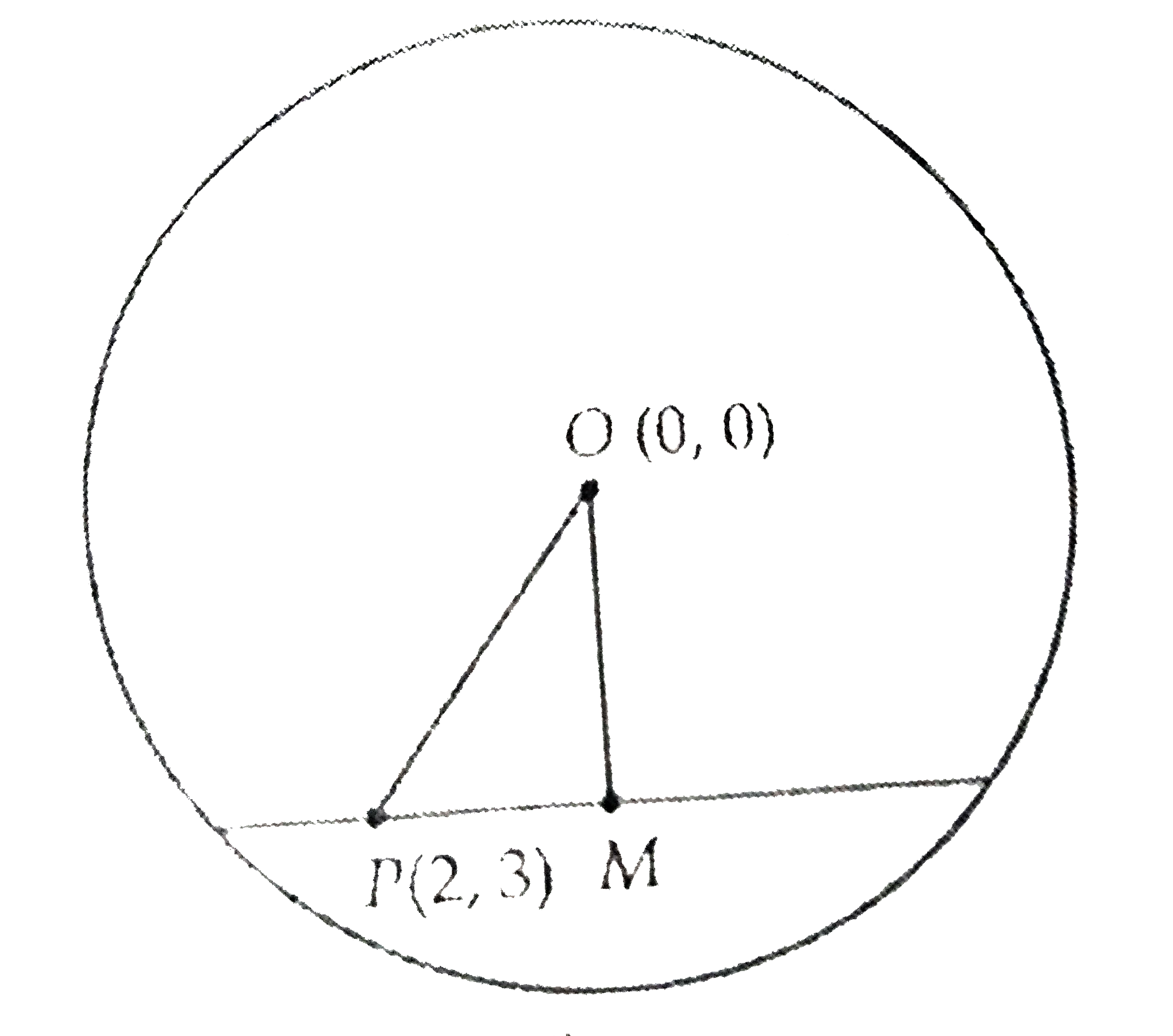
Let P(2, 3) be the given point and M be the mid-point of a chord through P.
In $Δ O M P$ , we have
$O P^{2} = O M^{2} + P M^{2} \Rightarrow O M = \sqrt{O P^{2} - P M^{2}}$
Clearly OM is maximum when PM is minimum i.e. M coincides with P i.e. P is the mid-point of the chord.
Chord PM passes through P(2, 3) and is perpendicular to OM.
So, its equation is $y - 3 = - \frac{2}{3} (x - 2)$ or, $2 x + 3 y = 13$ .

|

Updated on:21/07/2023

Class 12 MATHS CIRCLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
A chord of the circle $x^{2} + y^{2} = a^{2}$ passes through a fixed point (2,3). The chord which is farthest from the centre is
A $x - 2 y + 4 = 0$
B $x - y + 1 = 0$
C $3 x - y - 3 = 0$
D $2 x + 3 y - 13 = 0$
Question 2 - Select One
Find the equation of the tangent to the circle $x^{2} + y^{2} = 9$ , which passes through the point on the circle where x = 2 and y is positive.
A $\sqrt{5} y = 2 x - 9$
B $\sqrt{5} y = - 2 x + 9$
C $2 y = - \sqrt{5} x + 4 \sqrt{5}$
D $2 y = - \sqrt{5} x - 4 \sqrt{5}$

OBJECTIVE RD SHARMA-CIRCLES-Chapter Test

Home
Ask Doubt
Profile