Question

Find the equation of the ellipse whose focus is $S(\pm 1,-1),$ the corresponding directrix is $x-y+3=0,$ and eccentricity is 1/2. Also find its center, the second focus, the equation of the second directrix, and the length of latus rectum.

Explanation

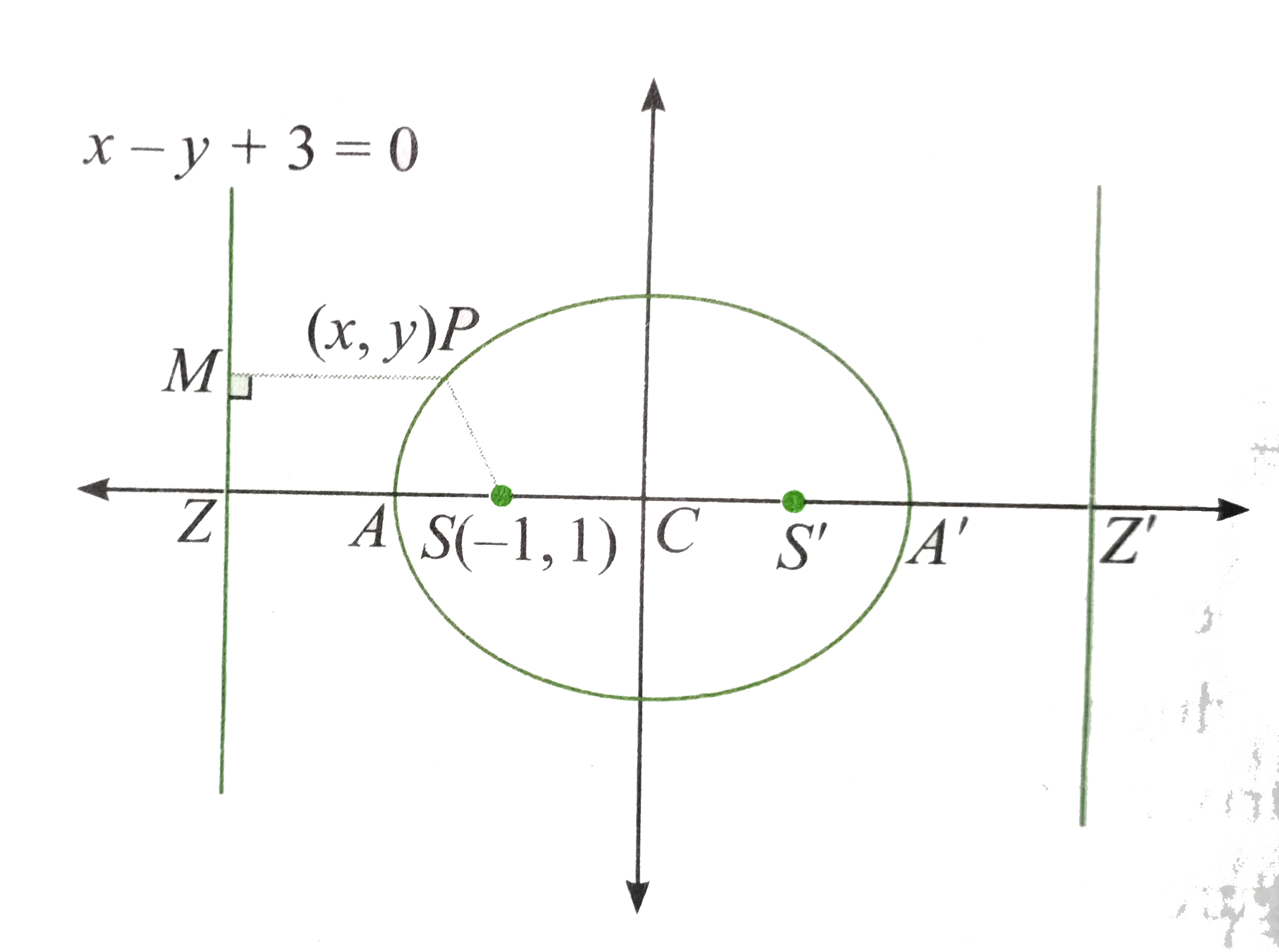
Let P(x,y) be any point on the ellips and PM be perpendicular to the directix , then PS= e, PM given
`sqrt((x+1)^(2)+(y-1)^(2))=(1)/(2)(|x-y+3|)/(sqrt(2))`
`rArr 7x^(2)+7y^(2)+2xy+10x-10y+7=0" ".....(1)`
The major axis passes through S(-1,1) and is perpendicular to directerix.
So, the equation of the major axis is `x+y=2 " " .....(2)`
Axis meets the directrix in Z,then coordinates of Z are (-3/2,3/2).
A divides ZS internally in the ratin `1: e or 1: 1//2 or 2:1`
`:. A-=(-7//6,7//6)`
A' divides ZS externally in the ratio `2:1`
`:. C'-=(-5//6,5//6)" ".....(3)`
Let other focus S' be (h,k)
Then `(1)/(2)(h-1)=-(5)/(6) and (1)//(2) and (1)/(2)(k+1)=(5)/(6)` (as C is midpoint of SS')
`:. S'-=(-2//3, 2//3)" ".....(4)`
If major axis meets the other diretrix at `Z'(alpha,beta)` then
`(1)/(2)(alpha-3//2)=-(5)/(6) and (1)/(2) (beta+3//2)=(5)/(6)`
`:. Z'-=(-1//6,1//6)`
The second directrix passes through `Z'(-1//6, 1//6)` and is perpendicular to the marjor axis.
Thus, the equation of other directrix is
`x-y+1//3=0" ".....(5)`
Also, length of L.R
`=2xxexx` distance of (-1,1) from the line `x-y+0`
`=2(1)/(2)(|-1-1+3|)/(sqrt(2))=(1)/(sqrt(2))`