Find the equation of the line which satisfy the given conditions : Perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive xaxis is 30o .
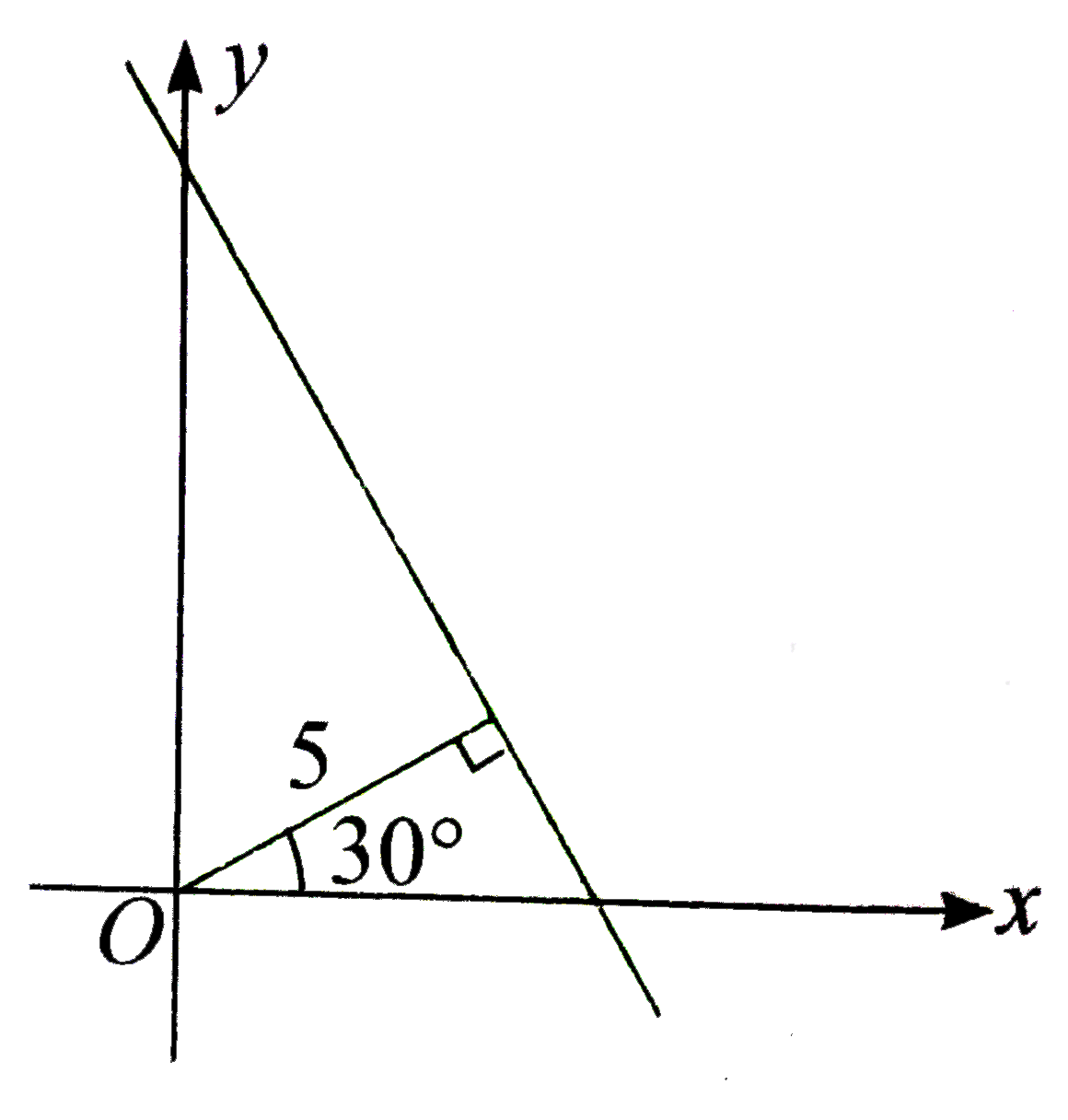
Data given in the question is for normal form of the line.
Standard equation of normal form is xcosα+ysinα=p.
∴p=5units and α=30∘.
Thus, the required equation of the given line is
xcos30∘+ysin30∘=5
or √3x+y=10
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.123videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINESEXERCISE - Exercise 2.24videos
STRAIGHT LINES
- BOOK - CENGAGECHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGECHAPTER - THEORY OF EQUATIONSEXERCISE - JEE Advanced Previous Year9videos
THEORY OF EQUATIONS
Similar Questions
Find the equation of the line whose perpendicular distance from the origin is 5 units and the angle made by the perpendicular with the positive X-axis is 30∘
View SolutionFind the equation of a line whose perpendicular distance from the origin is 2 units and the angle between the perpendicular segment and the positive of the x-axis is 240∘.
View Solution
Knowledge Check
- Question 1 - Select One
The equation of the line whose perpendicular distance from the origin is 3 units and the angle which the normal makes with with the positive direction of x -axis is 30∘ is
Ax+√3y=3B√3x+y=6C√3x+y=1Dx+√3y=6
Find the equation of the line whose perpendicular distance from the origin is 3 units and the angle between the positive direction of x-axis and the perpendicular is 15∘.
View SolutionFind the equation of the line upon which the length of perpendicular p from origin and the angle apha made by this perpendicular with the positive direction of x-axis are p=5,α=1350
View SolutionFind the equation of the line which satisfy the given conditions : Intersecting the xaxis at a distance of 3 units to the left of origin with slope 2.
View SolutionFind the equation of a line with slope –1 and whose perpendicular distance from the origin is equal to 5.
View SolutionFind the equation of the line on which the length of the perpendicular segment from the origin to the line is 4 and the inclination of the perpendicular segment with the positive direction of x-axis is 300.
View SolutionFind the equation of the line where the perpendicular distance p of the line from origin and the angle α made by the perpendicular with x-axis are given as: p=1,α900
View SolutionFind the equation of a line with slope −1 and whose perpendicular distance from the origin is equal to 5
View Solution