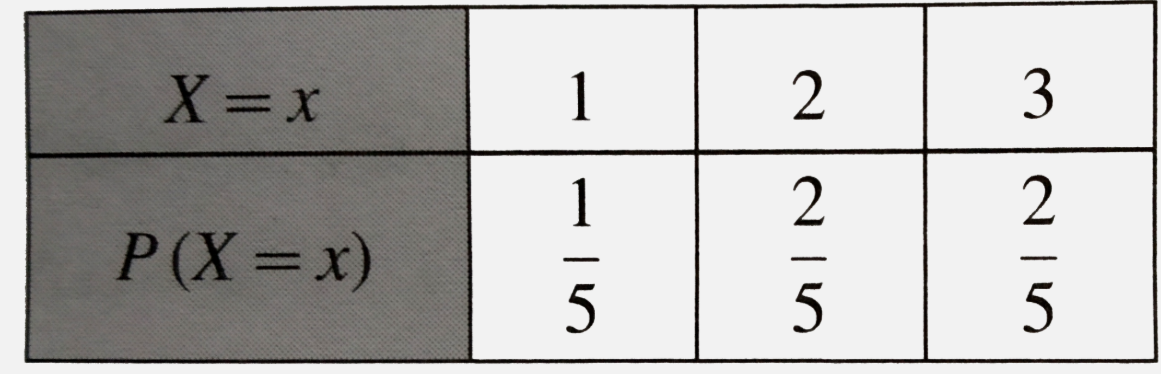
Find the expected value ,variance and standard deviation of random variable X whose probability mass function (p.m.f.) is given below.

Video Solution
Text Solution
Mean , E(X)=∑XP(X)
=1×15+2×25+3×25
=15+45+65=115
Variance (X)=∑X2P(X)−[E(X)]2
=12×15+22×25+32×25−(115)2
=15+85+185−12125=275−12125
=135−12125=1425
S.D √Variance
=√1425=3⋅745
0⋅748
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
A random variable X has the probability distribution given below
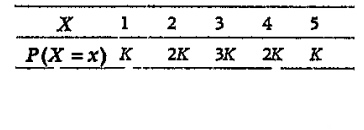
Its variance isA163B43C53D103If m and σ2 are the mean and variance of the random variable X, whose distribution is given by
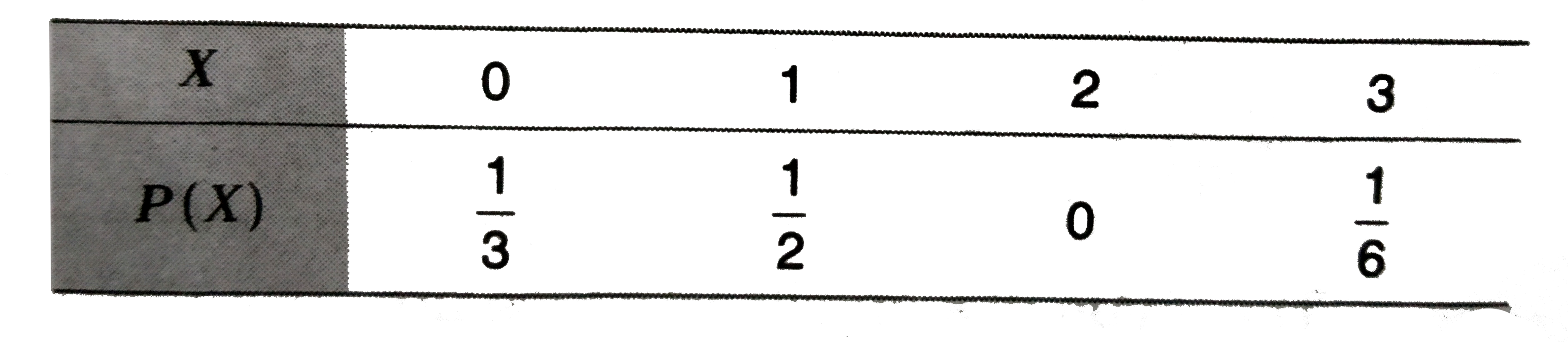
 Am=σ2=2Bm=1,σ2=2Cm=σ2=1Dm=2,σ2=1
Am=σ2=2Bm=1,σ2=2Cm=σ2=1Dm=2,σ2=1
A random variable X has the probability distribution given below
Its variance is

View SolutionFind expected value of the random Variable X whose probability mass function is X=x,1,2,3<br>P(X=x)15,25,25
View SolutionA random variable X has the following probability distribution find K.

View SolutionA random variable X has the follwing probability distribution:

Find k.
View SolutionIf m and σ2 are the mean and variance of the random variable X whose distribution is given by
View SolutionFind the expected value and variance of X using the following p.m. f.

View Solution