Find the image of interval [−1,3] under the mapping specified by the function f(x)=4x3−12x.
A
[8,72]
B
[−8,72]
C
[0,8]
D
[8,−72]
Video Solution
Text Solution
The correct Answer is:B
We have
f(x)=4x3−12x⇒f'(x)=12(x−1)(x+1)
The signs of f' (x) are shown in the following figure:
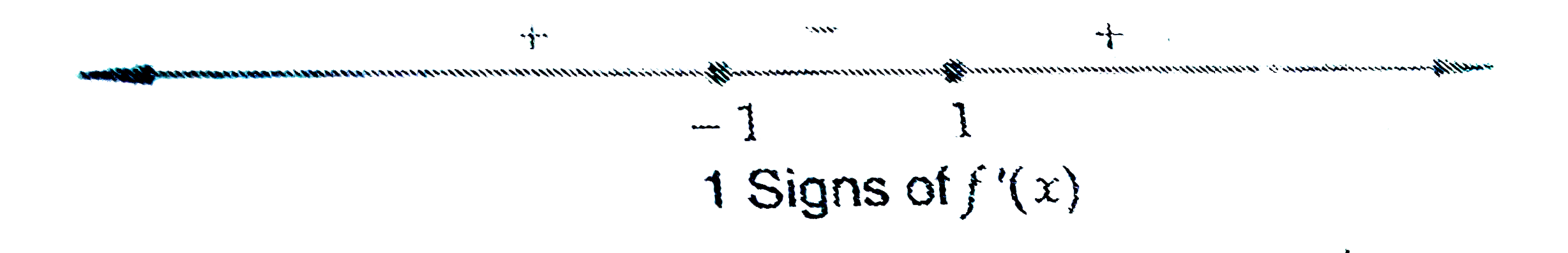
Clearfy, f'(x)<0for x∈(−1,1)andf'(x)>0for x→(1,3)
f(x)in [−1,3]is f(1)=−8
Greatest value of f(x)in [−1,3] isf(3)=72
f(x) is continous on [−1,3]. So, it attains every value between its minimum and maximum values.
Hence, Range of f=[−8,72]=Image of =[1,3] under f.
|
Topper's Solved these Questions
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Section I - Solved Mcqs
49 Videos
- FUNCTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - FUNCTIONSEXERCISE - Section II - Assertion Reason Type
10 Videos
- DISCRETE PROBABILITY DISTRIBUTIONSBOOK - OBJECTIVE RD SHARMACHAPTER - DISCRETE PROBABILITY DISTRIBUTIONSEXERCISE - Exercise
40 Videos
- HYPERBOLABOOK - OBJECTIVE RD SHARMACHAPTER - HYPERBOLAEXERCISE - Chapter Test
29 Videos
Similar Questions
Knowledge Check
In the interval (-1, 1), the function f(x)=x2−x+4 is :
AincreasingBdecreasingCneither increasing nor decreasingDNone of the above
Find the domain of the function: f(x)=cos−1(6−3x4)+cosec−1(x−12)
View SolutionFind the image of the following sets under the mapping f(x)=x4−8x3+22x2−24x+10 (i) (−∞,1)
View SolutionFind all the points of local maxima and minima of the function f given by f(x)=4x3−12x2+12x+10
View SolutionFind the interval of monotonocity of the function f(x)=|x−1|x2.
View SolutionFind the value of c in Mean Value theorem for the function f(x)=2x+33x−2 in the interval [1,5].
View SolutionDetermine the intervals of increase and decrease for the following functions :
f(x)=13x3−1x
View SolutionFind the intervals in which the function f(x)=x3−12x2+36x+117 is increasing
View Solution
