Find the image of point (1,2,3) in the line x−63=y−72=z−7−2.Solution in Bengali
Let the image of point A(1,2,3) in the line l whose equation is
x−63=y−72=z−7−2=k (say) (i)
be A'. Then ∀' is perpendicular to l and the point of intersection of ∀' and l is the midpoint of ∀'. Note that M is the foot of perpendicular from A to l.
The coordinates of any point on the given line are of the form (3k+6,2k+7,−2k+7). Therefore, the coordinates of M are 3k+6,2k+7and−2k+7 for some value of k. The direction ratios of AM are 3k+6−1,2k+7−2and−2k+7−3or3k+5,2k+5,−2k+4.
Also, the direction ratios of l are 3, 2 and -2.
since AM⊥l,a1a2+b1b2+c1c2=0.
⇒ 3(3k+5)+2(2k+5)−2(−2k+4)=0
or 17k+17=0ork=−1
Thus, the coordinates of M are 3, 5 and 9.
Suppose coordinates of A' are x,yandz,
The coordinates of the midpoint of ∀' are
x+12,y+22andz+32 .
But the midpoint of ∀' is (5, 3, 9). Therefore,
x+12=3,y+22=5andz+32=9
⇒ x=5,y=8,z=15
Thus, the image of A in l is (5, 8, 15).
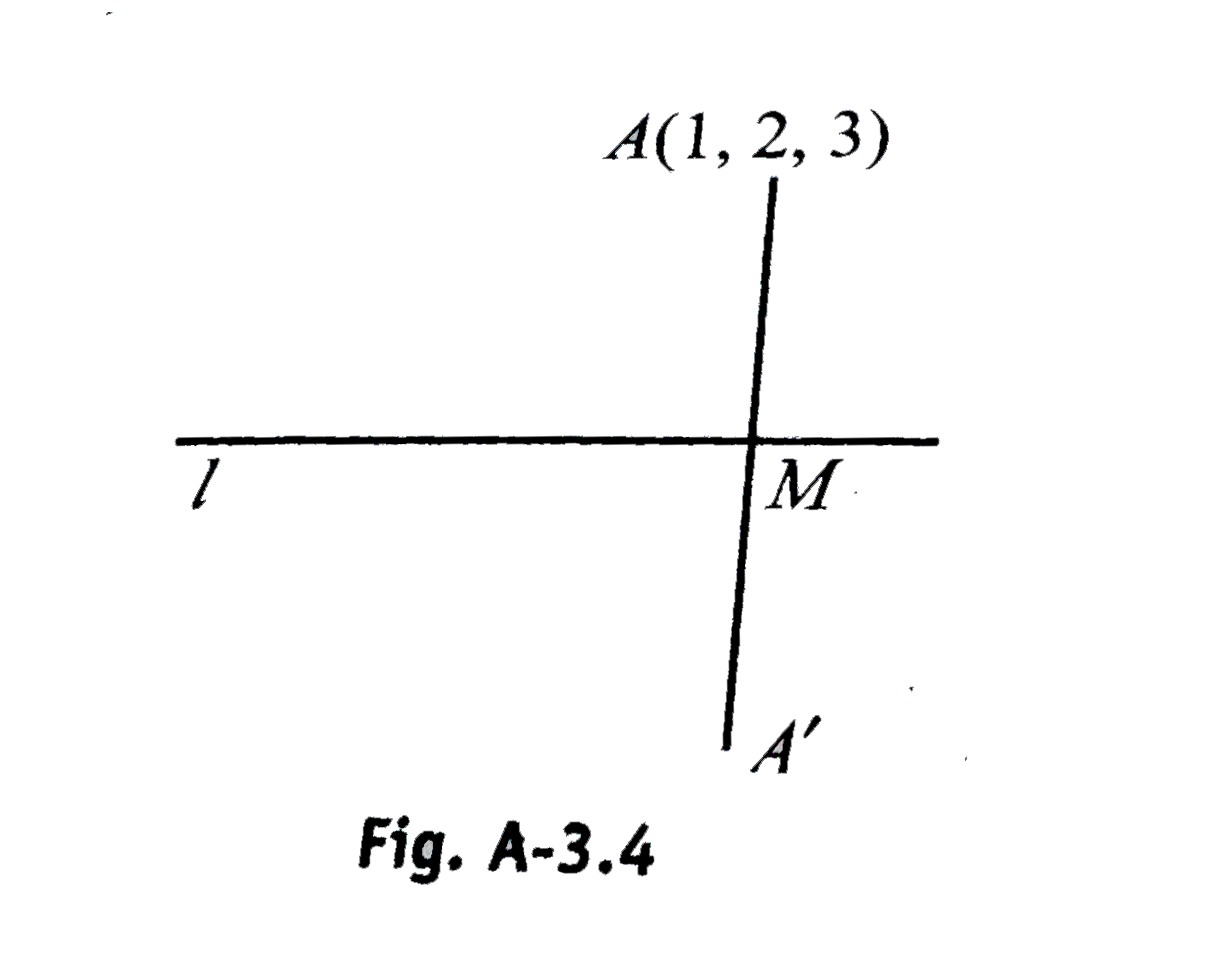
Topper's Solved these Questions
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.3
19 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.4
5 Videos
- THREE-DIMENSIONAL GEOMETRY BOOK - CENGAGE PUBLICATIONCHAPTER - THREE-DIMENSIONAL GEOMETRY EXERCISE - CONCEPT APPLICATION EXERCISE 3.1
12 Videos
- THREE DIMENSIONAL GEOMETRYBOOK - CENGAGE PUBLICATIONCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - All Questions
291 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
Similar Questions
Find the angle between the line x−13=y−12=z−14 and the plane 2x+y−3z+4=0.
View SolutionFind the plane of the intersection of x2+y2+z2+2x+2y+2=0 and 4x2+4y2+4z2+4x+4y+4z−1=0.
View SolutionIf the x-coordinate of a point on the join of P(2,2,1)andQ(5,1,−2)is4, then find its z− coordinate.
View SolutionFind the angle between the line whose direction cosines are given by l+m+n=0andl2+m2−n2=0.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionFind the length of the perpendicular from the point (1,2,3) to the line x−63=y−72=z−7−2.
View Solutionबिन्दु (1,2,3) से रेखा x−63=y−72=z−7−2 पर डाले गये लम्ब की लम्बाई है-
View SolutionFind the image of the point (1,2,3) in the line x−63=y−72=z−7−2.
View SolutionFind the distance of the point (1,2,3) from the line x−62=y−72=z−7−3.
View SolutionFind the foot of perpendicular drawn from the point P (1,2,3) on the line x−63=y−72=7−z2. Also find the equation of the plane containing the line and the point (1,2,3).
View Solutionबिन्दु (1,2,3) से रेखा x−63=y−72=z−7−2 पर लम्ब की लम्बाई है
View Solutionबिन्दु (1,2,3) से रेखा x−63=y−72=z−7−2 पर खींचे गए लम्ब की लम्बाई है
View SolutionFind the image of the point (1,2,3) in the line x−63=y−72=z−7−2.
View SolutionFind the image of point (1,2,3) in the line x−63=y−72=z−7−2.
View SolutionFind the length of the perpendicular from the point (1,2,3) to the line x−63=y−72=z−7−2.
View SolutionFind the image of point (0, 3, 7) in the line x−43=y+32=z−6−1
View Solution
