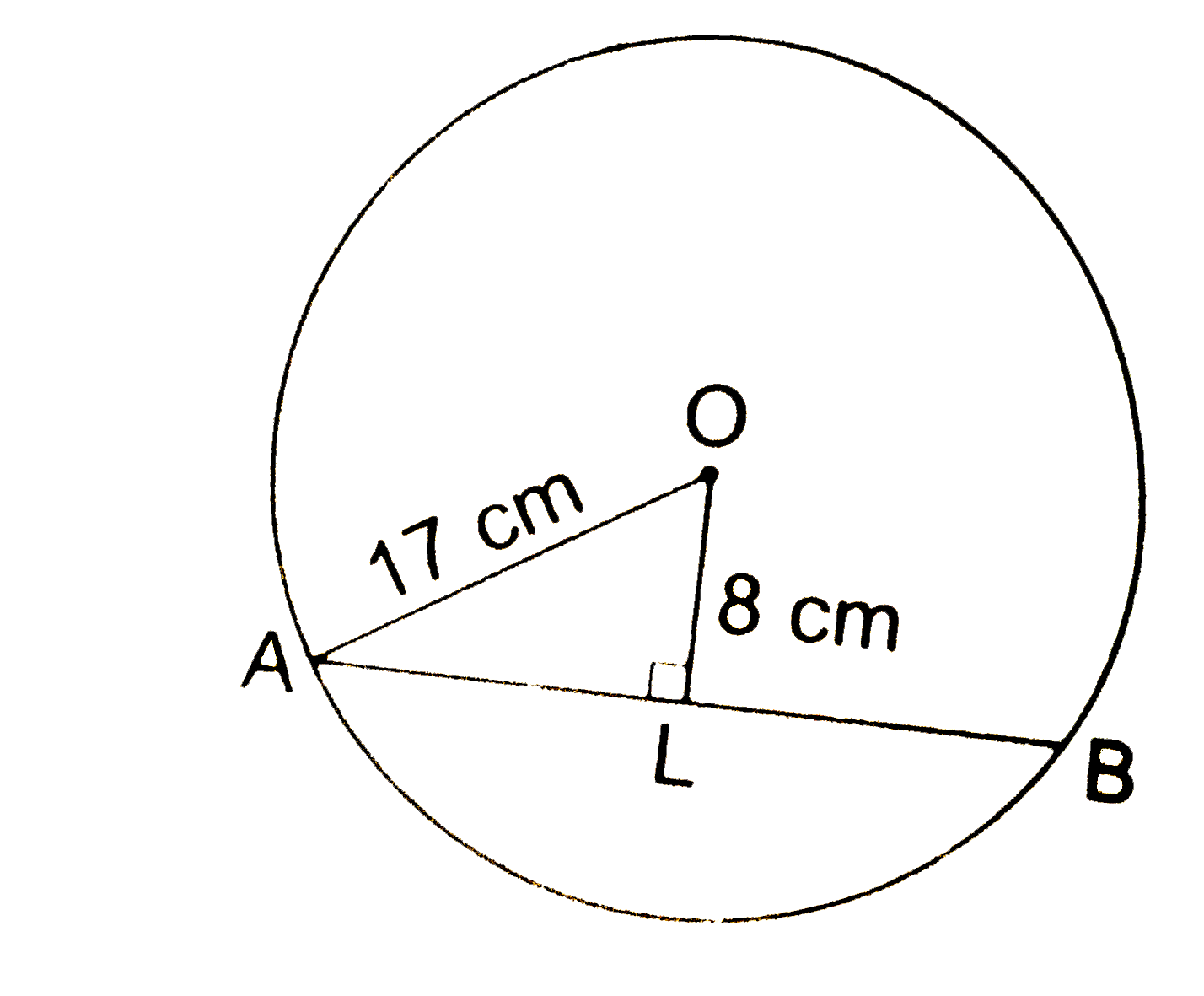
Find the length of a chord which is at a distance of 8cm from the centre of a circle of radius 17cm.
A
25cm
B
35cm
C
30cm
D
None
Video Solution
Text Solution
The correct Answer is:C
Let AB be a chord of a circle with centre O and radius 17cm.
Draw OL ⊥ AB. Join OA.
Then , OL=8cm and OA=17cm.
From the right ΔOLA , we have
OA2=OL2+AL2
⇒AL2=OA2−OL2=[(17)2−(8)2]cm2
=(17+8)(17−8)cm2=225cm2
⇒AL=√225=15cm.
Since the perpendicular fromthe centre of a circle to a chord bisects the chord, we have
AB=2×AL=(2×15)cm=30cm
|
Similar Questions
Knowledge Check
In a circle of radius 13 cm , a chord is at a distance of 12 cm from the centre of the circle. What is the length of the chord?
13 सेमी त्रिज्या वाले एक वृत्त में, वृत्त के केंद्र से 12 सेमी की दूरी पर एक जीवा है | जीवा की लंबाई ज्ञात करें |A10 cm.B5 cm.C6 cm.D12 cm.A chord 6 cm long is at a distance of 4 cm from the centre of a circle. Find the length of a chord which is at a distance of 3 cm from the centre of the circle.
A10 cmB6 cmC8 cmD12 cmA chord is at a distance of 8 cm from the centre of a circle of radius 17 cm. The length of the chord is
A25cmB12.5cmC30cmD9cm
Find the length of a chord which is at a distance of 5 cm from the centre of a circle of radius 13 cm.
View SolutionFind the length of a chord which is at a distance of3 cm from the centre of a circle of radius 5 cm.
View Solution(i) Find the length of a chord which is at a distance of 12 cm from the centre of a circle of radius 13cm.
(ii) The length of a chord is 16 cm of a circle of diameter 2 cm. find the perpendicular distance of this chord from the centre of the circle.
View SolutionFind the length of a chord which is at a distance of 4 cm from the centre of the circle of radius 6 cm.
View SolutionThe length (in cm) of a chord which is at a distance of 8 cm from the centre of a circle of radius 17 cm____
View Solution