Find the length of altitude through A of the triangle ABC, where A≡(−3,0)B≡(4,−1),C≡(5,2)
The correct Answer is:22√10
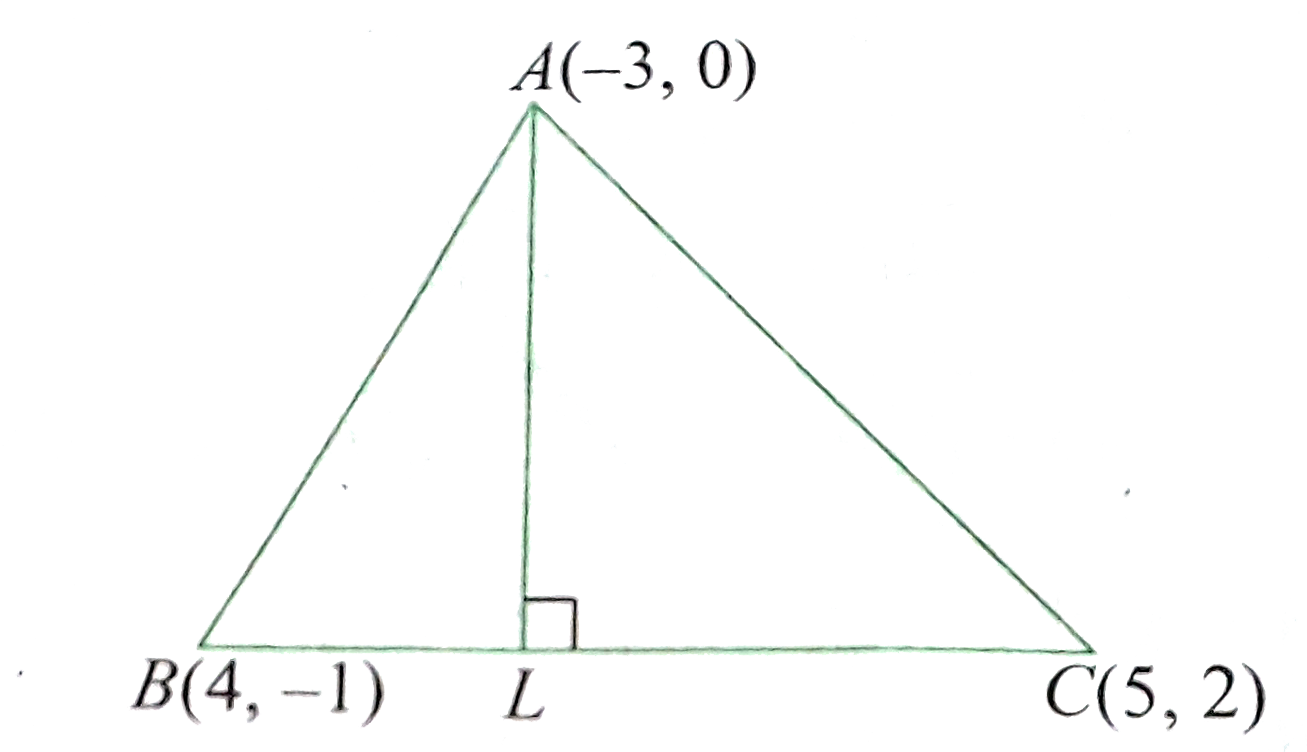
In the figure , AL is altitude .
Area of triangle =12[−3(−1−2)+4(2−0)+5(0+1)]=11
Also, BC=√(5−4)2+(2+1)2=√1+9=√10
Now, area of triangle =12×AL×BC
∴AL=2×11√10=22√10 .
Topper's Solved these Questions
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.3
Explore 10 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.4
Explore 8 Videos
- COORDINATE SYSYEM Book:CENGAGEChapter:COORDINATE SYSYEM Exercise:Exercise 1.1
Explore 6 Videos
- COORDINATE SYSTEMBook:CENGAGEChapter:COORDINATE SYSTEMExercise:Multiple Correct Answers Type
Explore 2 Videos
- CROSS PRODUCTS Book:CENGAGEChapter:CROSS PRODUCTS Exercise:DPP 2.2
Explore 13 Videos
Similar Questions
Find the length of altitude through A of the triangle ABC, where A≡(−3,0)B≡(4,−1),C≡(5,2)
View SolutionFind the lengths of the altitudes of the triangle whose vertices are A(1,3),B(5,-6) and C(7,-4) ,
View SolutionFind the length of the median AM of the triangle with vertices A(1,−1),B(0,4), and C(−5,3) .
View SolutionFind the equations of the altitudes of a △ABC, whose vertices are A(2,-2), B(1,1) and C(-1,0).
View SolutionFind the lengths of the medians of the triangle with vertices A(0,0,6), B(0,4,0)and C(6,0,0).
View SolutionFind the length of the medians of the triangle with vertices A(0, 0, 3), B(0, 4, 0) and C (5, 0, 0).
View SolutionFind the equation of the altitudes of the triangle whose vertices are A(7,−1),B(−2,8)andC(1,2).
View SolutionFind the equations to the altitudes of the triangle whose angular points are A(2,−2),B(1,1) and C(−1,0).
View SolutionFind the lengths of the medians of a triangle whose vertices are A(−1,1),B(5,−3) and C(3,6)
View SolutionFind the lengths of the medians of triangle whose vertices are
A (-1,1) , B (5,-3) and C (3,5).
View Solution