Find the locus of the center of the circle touching the circle x2+y2−4y=4 internally and tangents on which from (1, 2) are making of 600 with each other.Solution in Tamil
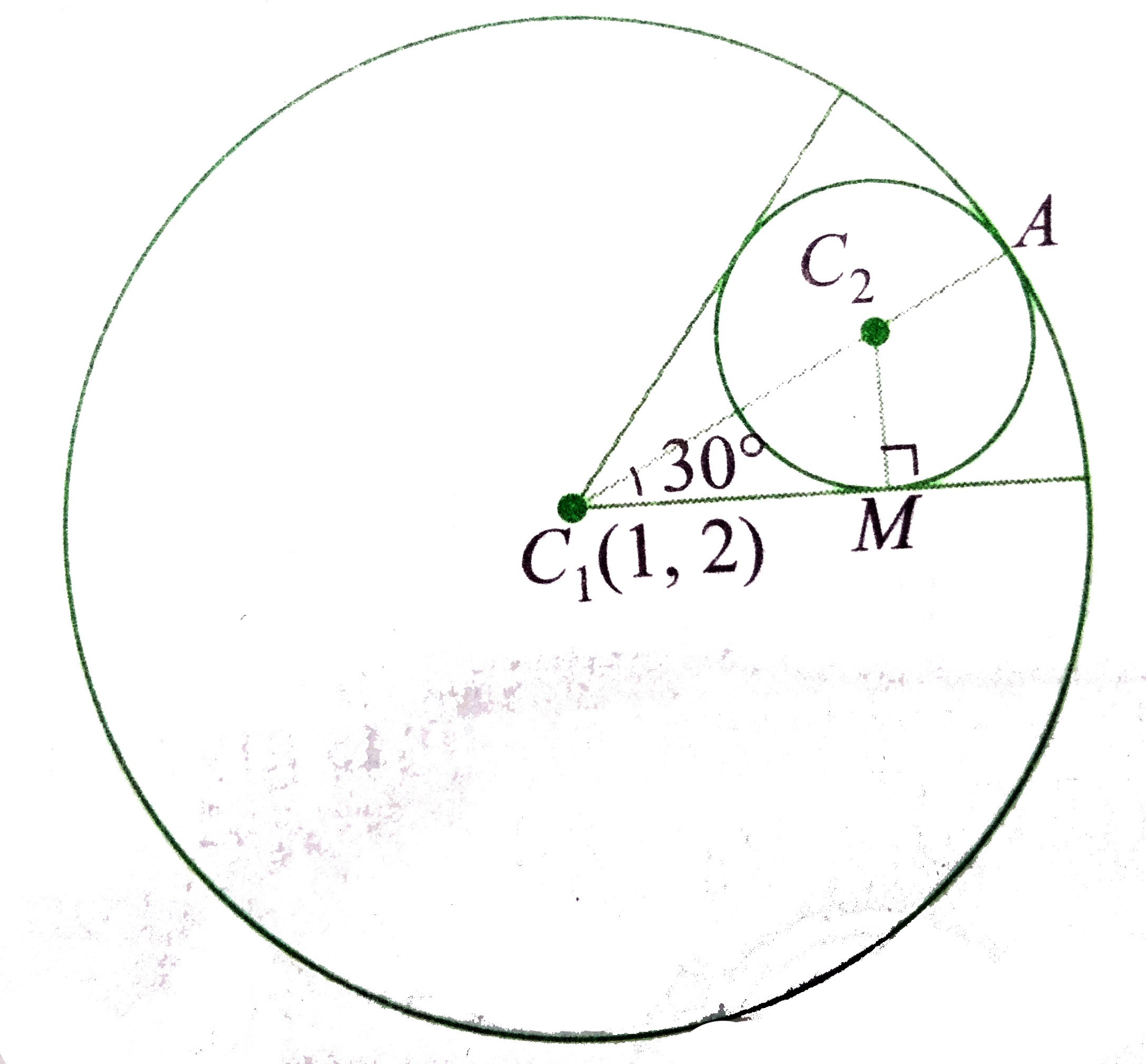
Given circle is x2+y2−4y−2x−4=0
Centre is C1(1,2) and radius is r1=√(−2)2+(−1)2−(−4)=3.
Let the centre of the variable circles touching given circle be C2(h,k).
Angle between tangents drawn from C1(1,2) to variable circle is 60∘.
In triangle C1MC2.
sin30∘=C2MC1C2
⇒sin30∘=C2AC1C2
⇒12=C1A−C1C2C1C2=3−C1C2C1C2
⇒C1C2=2
⇒√(h−1)2+(k−2)2=2
Therefore, required locus is (x−1)2+(y−2)2=4.
Topper's Solved these Questions
Similar Questions
If a circle whose center is (1,−3) touches the line 3x−4y−5=0 , then find its radius.
05:03View SolutionFind the radius of the circle (x−5)(x−1)+(y−7)(y−4)=0 .
02:44View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is07:31View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe locus of the centre of a circle touching the circle x^(2)+y^(2)-4y-2x=2sqrt(3)-1 internally and tangents on which from (1,2) is making a 60^(@) angle with each other is a circle. then integral part of its radius is
05:35View SolutionFind the locus of the center of the circle touching the circle x2+y2−4y−2x=4 internally and tangents on which from (1, 2) are making of 600 with each other.
09:34View SolutionIf 3x+y=0 is a tangent to a circle whose center is (2,−1) , then find the equation of the other tangent to the circle from the origin.
10:27View Solutionएक वृत्त x -अक्ष को स्पर्श करता है और एक-दूसरे वृत्त को भी स्पर्श करता है जिसका केंद्र (0,3) है तथा त्रिज्या 2 है। इस वृत्त के केंद्र के बिन्दुपथ का समीकरण निम्न में से क्या है?
03:29View SolutionShow that the circles x2+y2−8x−4y−16=0 and x2+y2−2x+4y+4=0 touch each other internally and find the coordinates of their point of contact.
04:56View SolutionProve that the circles x2+y2+4x−10y−20=0 and x2+y2−4x−4y+4=0 touch each other internally. Find the equation of their common tangent.
02:44View Solutionदर्शाइए कि वृत्त
x2+y2−2x−4y=0
और x2+y2−8y−4=0
एक - दूसरे को अन्तः स्पर्श करते है ।02:41View SolutionA circle touches the x-axis and also touches each other whose center is (0, 3) and radius is 2. Which of the following is the equation of the locus of the center of that circle?
04:29View SolutionLocus of the point of intersection of tangents to the circle x2+y2+2x+4y−1=0 which include an angle of 602 is
06:43View SolutionFind the locus of the center of the circle touching the circle x2+y2−4y−2x=4 internally and tangents on which from (1, 2) are making of 600 with each other.
05:02View SolutionIf 3x+y=0 is a tangent to a circle whose center is (2,−1) , then find the equation of the other tangent to the circle from the origin.
03:24View SolutionFind the locus of the center of the circle touching the circle x2+y2−4y−2x=4 internally and tangents on which from (1, 2) are making of 600 with each other.
05:52View Solution

