Find the mean and variance for each of the data :
To find the mean and variance of the first 10 multiples of 3, we can follow these steps:
Step 1: Identify the Data
The first 10 multiples of 3 are:
- 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
Step 2: Calculate the Mean (x̄)
The mean is calculated using the formula:
¯x=Σxin
where Σxi is the sum of all data points and n is the number of data points.
Calculating the sum:
Σxi=3+6+9+12+15+18+21+24+27+30
Calculating the sum:
Σxi=3+6=99+9=1818+12=3030+15=4545+18=6363+21=8484+24=108108+27=135135+30=165
Thus, Σxi=165.
Calculating the mean:
n=10¯x=16510=16.5
Step 3: Calculate the Variance (σ²)
Variance is calculated using the formula:
σ2=Σ(xi−¯x)2n
Calculating (xi−¯x)2:
- For x1=3: (3−16.5)2=(−13.5)2=182.25
- For x2=6: (6−16.5)2=(−10.5)2=110.25
- For x3=9: (9−16.5)2=(−7.5)2=56.25
- For x4=12: (12−16.5)2=(−4.5)2=20.25
- For x5=15: (15−16.5)2=(−1.5)2=2.25
- For x6=18: (18−16.5)2=(1.5)2=2.25
- For x7=21: (21−16.5)2=(4.5)2=20.25
- For x8=24: (24−16.5)2=(7.5)2=56.25
- For x9=27: (27−16.5)2=(10.5)2=110.25
- For x10=30: (30−16.5)2=(13.5)2=182.25
Summing these squared differences:
Σ(xi−¯x)2=182.25+110.25+56.25+20.25+2.25+2.25+20.25+56.25+110.25+182.25
Calculating the sum:
=182.25+110.25=292.5292.5+56.25=348.75348.75+20.25=369369+2.25=371.25371.25+2.25=373.5373.5+20.25=393.75393.75+56.25=450450+110.25=560.25560.25+182.25=742.5
Thus, Σ(xi−¯x)2=742.5.
Calculating the variance:
σ2=742.510=74.25
Final Results
- Mean (x̄) = 16.5
- Variance (σ²) = 74.25
The first 10 multiples of 3 are:
- 3, 6, 9, 12, 15, 18, 21, 24, 27, 30
The mean is calculated using the formula:
¯x=Σxin
where Σxi is the sum of all data points and n is the number of data points.
Σxi=3+6+9+12+15+18+21+24+27+30
Calculating the sum:
Σxi=3+6=99+9=1818+12=3030+15=4545+18=6363+21=8484+24=108108+27=135135+30=165
Thus, Σxi=165.
n=10¯x=16510=16.5
Variance is calculated using the formula:
σ2=Σ(xi−¯x)2n
- For x1=3: (3−16.5)2=(−13.5)2=182.25
- For x2=6: (6−16.5)2=(−10.5)2=110.25
- For x3=9: (9−16.5)2=(−7.5)2=56.25
- For x4=12: (12−16.5)2=(−4.5)2=20.25
- For x5=15: (15−16.5)2=(−1.5)2=2.25
- For x6=18: (18−16.5)2=(1.5)2=2.25
- For x7=21: (21−16.5)2=(4.5)2=20.25
- For x8=24: (24−16.5)2=(7.5)2=56.25
- For x9=27: (27−16.5)2=(10.5)2=110.25
- For x10=30: (30−16.5)2=(13.5)2=182.25
Σ(xi−¯x)2=182.25+110.25+56.25+20.25+2.25+2.25+20.25+56.25+110.25+182.25
Calculating the sum:
=182.25+110.25=292.5292.5+56.25=348.75348.75+20.25=369369+2.25=371.25371.25+2.25=373.5373.5+20.25=393.75393.75+56.25=450450+110.25=560.25560.25+182.25=742.5
Thus, Σ(xi−¯x)2=742.5.
σ2=742.510=74.25
- Mean (x̄) = 16.5
- Variance (σ²) = 74.25
Topper's Solved these Questions
Similar Questions
Find the mean and variance for each of the data in Question:
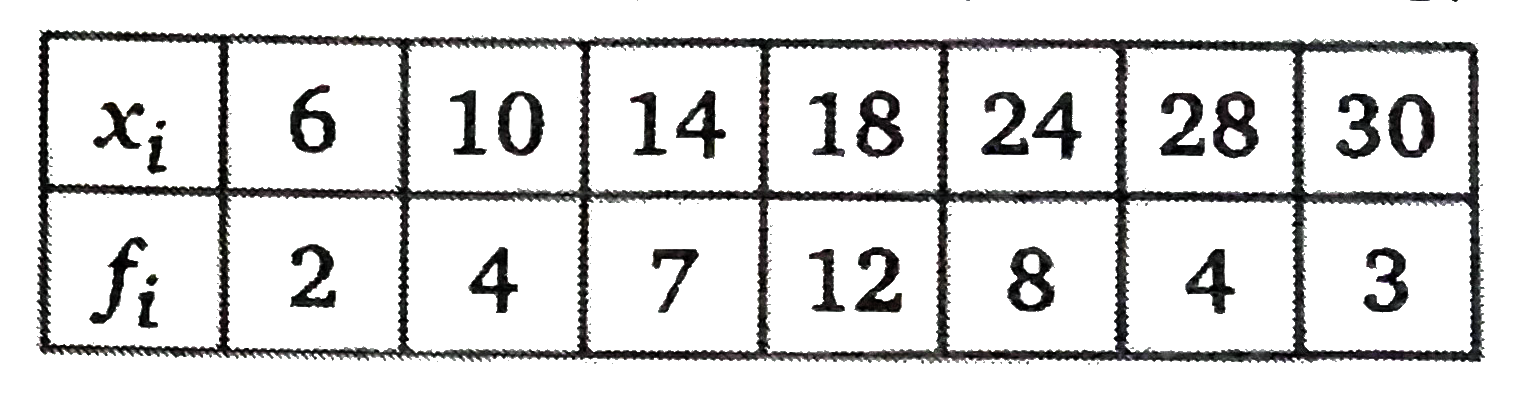
View SolutionFind the mean and variance for each of the data in Question:

View SolutionFind the mean and variance for each of the data :
First n natural numbers
View SolutionFind the mean and variance for each of the data : 6,7,10,12,13,4,8,12
View SolutionFind the sum of first 10 multiples of 3,
View SolutionFind the sum of first 10 multiples of 6.
View SolutionFind the sum of first 10 multiples of 6.
View SolutionFind the sum of first 10 multiples of 6.
View SolutionFind the S.D. and variance of the following data:

View SolutionFind the sum of first 8 multiples of 3.
View Solution