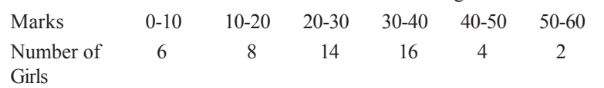Find the mean deviation about the mean for the following data: Marks obtained 10-20 20-30 30-40 40-50 50-60 60-70 70-80 Number of students 2 3 8 14 8 3 2
To find the mean deviation about the mean for the given data, we will follow these steps:
Step 1: Create a frequency distribution table
We will list the class intervals and the corresponding number of students (frequencies).
| Marks Obtained | Number of Students (f) |
|----------------|------------------------|
| 10 - 20 | 2 |
| 20 - 30 | 3 |
| 30 - 40 | 8 |
| 40 - 50 | 14 |
| 50 - 60 | 8 |
| 60 - 70 | 3 |
| 70 - 80 | 2 |
Step 2: Calculate the mid-values (x_i) of each class interval
The mid-value for each class interval can be calculated as:
xi=Lower limit+Upper limit2
| Marks Obtained | Mid-value (x_i) | Number of Students (f) |
|----------------|------------------|------------------------|
| 10 - 20 | 15 | 2 |
| 20 - 30 | 25 | 3 |
| 30 - 40 | 35 | 8 |
| 40 - 50 | 45 | 14 |
| 50 - 60 | 55 | 8 |
| 60 - 70 | 65 | 3 |
| 70 - 80 | 75 | 2 |
Step 3: Calculate the total number of students (N)
N=∑f=2+3+8+14+8+3+2=40
Step 4: Calculate the mean (x̄)
The mean can be calculated using the formula:
¯x=∑(f⋅xi)N
Calculating f⋅xi:
| Marks Obtained | Mid-value (x_i) | Number of Students (f) | f * x_i |
|----------------|------------------|------------------------|---------|
| 10 - 20 | 15 | 2 | 30 |
| 20 - 30 | 25 | 3 | 75 |
| 30 - 40 | 35 | 8 | 280 |
| 40 - 50 | 45 | 14 | 630 |
| 50 - 60 | 55 | 8 | 440 |
| 60 - 70 | 65 | 3 | 195 |
| 70 - 80 | 75 | 2 | 150 |
Now summing f⋅xi:
∑(f⋅xi)=30+75+280+630+440+195+150=1800
Calculating the mean:
¯x=180040=45
Step 5: Calculate the deviations from the mean (d_i)
We calculate di=xi−¯x and take the absolute value.
| Mid-value (x_i) | d_i (x_i - x̄) | |d_i| |
|------------------|----------------|------|
| 15 | 15 - 45 = -30 | 30 |
| 25 | 25 - 45 = -20 | 20 |
| 35 | 35 - 45 = -10 | 10 |
| 45 | 45 - 45 = 0 | 0 |
| 55 | 55 - 45 = 10 | 10 |
| 65 | 65 - 45 = 20 | 20 |
| 75 | 75 - 45 = 30 | 30 |
Step 6: Calculate f⋅|di|
Now we calculate f⋅|di|:
| Marks Obtained | Number of Students (f) | |d_i| | f * |d_i| |
|----------------|------------------------|------|---------|
| 10 - 20 | 2 | 30 | 60 |
| 20 - 30 | 3 | 20 | 60 |
| 30 - 40 | 8 | 10 | 80 |
| 40 - 50 | 14 | 0 | 0 |
| 50 - 60 | 8 | 10 | 80 |
| 60 - 70 | 3 | 20 | 60 |
| 70 - 80 | 2 | 30 | 60 |
Now summing f⋅|di|:
∑(f⋅|di|)=60+60+80+0+80+60+60=400
Step 7: Calculate the mean deviation (MD)
The mean deviation is calculated as:
MD=∑(f⋅|di|)N=40040=10
Final Answer
The mean deviation about the mean for the given data is 10.
---
We will list the class intervals and the corresponding number of students (frequencies).
|----------------|------------------------|
| 10 - 20 | 2 |
| 20 - 30 | 3 |
| 30 - 40 | 8 |
| 40 - 50 | 14 |
| 50 - 60 | 8 |
| 60 - 70 | 3 |
| 70 - 80 | 2 |
The mid-value for each class interval can be calculated as:
xi=Lower limit+Upper limit2
|----------------|------------------|------------------------|
| 10 - 20 | 15 | 2 |
| 20 - 30 | 25 | 3 |
| 30 - 40 | 35 | 8 |
| 40 - 50 | 45 | 14 |
| 50 - 60 | 55 | 8 |
| 60 - 70 | 65 | 3 |
| 70 - 80 | 75 | 2 |
N=∑f=2+3+8+14+8+3+2=40
The mean can be calculated using the formula:
¯x=∑(f⋅xi)N
|----------------|------------------|------------------------|---------|
| 10 - 20 | 15 | 2 | 30 |
| 20 - 30 | 25 | 3 | 75 |
| 30 - 40 | 35 | 8 | 280 |
| 40 - 50 | 45 | 14 | 630 |
| 50 - 60 | 55 | 8 | 440 |
| 60 - 70 | 65 | 3 | 195 |
| 70 - 80 | 75 | 2 | 150 |
∑(f⋅xi)=30+75+280+630+440+195+150=1800
¯x=180040=45
We calculate di=xi−¯x and take the absolute value.
|------------------|----------------|------|
| 15 | 15 - 45 = -30 | 30 |
| 25 | 25 - 45 = -20 | 20 |
| 35 | 35 - 45 = -10 | 10 |
| 45 | 45 - 45 = 0 | 0 |
| 55 | 55 - 45 = 10 | 10 |
| 65 | 65 - 45 = 20 | 20 |
| 75 | 75 - 45 = 30 | 30 |
Now we calculate f⋅|di|:
|----------------|------------------------|------|---------|
| 10 - 20 | 2 | 30 | 60 |
| 20 - 30 | 3 | 20 | 60 |
| 30 - 40 | 8 | 10 | 80 |
| 40 - 50 | 14 | 0 | 0 |
| 50 - 60 | 8 | 10 | 80 |
| 60 - 70 | 3 | 20 | 60 |
| 70 - 80 | 2 | 30 | 60 |
∑(f⋅|di|)=60+60+80+0+80+60+60=400
The mean deviation is calculated as:
MD=∑(f⋅|di|)N=40040=10
The mean deviation about the mean for the given data is 10.
Topper's Solved these Questions
Similar Questions
Knowledge Check
Find the mean deviation (approximately) about the mode for the following ungrouped data: 20, 25, 30, 18, 15, 40.
A6.71B4.52C7.61D5.33
Calculate the median deviation from the median of the following data: Wages per week (in Rs.), 10-20, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80 No. of workers, 4, 6, 10, 20, 10, 6, 4
View SolutionFind the mean deviation about arithmetic mean of the following frequency distribution.Marks 0−10,10−20,20−30,30−40,40−50 No. of Students 5,8,15,16,6
View SolutionCalculate the mean devation from the mean the following data:
Marks0−1010−2020−3030−4040−50No. of stu.5815166
View SolutionObtain the mean , median and mode of the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 5 7 15 25 20 15 8 5
View SolutionFind the standard deviation for the following data:
10, 20, 30, 40, 50, 60, 70, 80, 90
View SolutionCaculate the median and mode from the following data :
Marks0−1010−2020−3030−4040−5050−6060−7070−80Number of Students 2 18 30 45 35 20 6 3
View SolutionCalculate the mean and standard deviation for the following distribution: Marks:, 20-30, 30-40, 40-50, 50-60, 60-70, 70-80, 80-90 No. of students:, 3, 6, 13, 15, 14, 5, 4
View Solution