Find the mean number of heads in three tosses of a fair coin.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:N/a

Probability of getting head or tail in a toss of one coin is
$P (H) = P (T) = \frac{1}{2}$
Sample space in three throw of an unbiased coin is
$S = {HH,HHT,HTH,THH,THT,TTH,HTT,TTT}$
The possible values of random variable $X$ are 0,1,2 or 3.
$∴ P (X = 0) = P$ (getting all tails)
$= P {TTT} = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}$
$P (X = 1) = P$ (getting one head and two tails)
$= P (TTH) + P (T H T) + P (HTT)$
$= \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$
$= \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{3}{8}$
$P (X = 2) = P$ (getting two heads and one tail)
$P (H H T) + P (H T H) + P (T H H)$
$= \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} + \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2}$
$= \frac{1}{8} + \frac{1}{8} + \frac{1}{8} = \frac{3}{8}$
$P (X = 3) = P$ (gettting three heads)
$= P (HHH) = \frac{1}{2} \times \frac{1}{2} \times \frac{1}{2} = \frac{1}{8}$
Therefore the required probability distribution is:

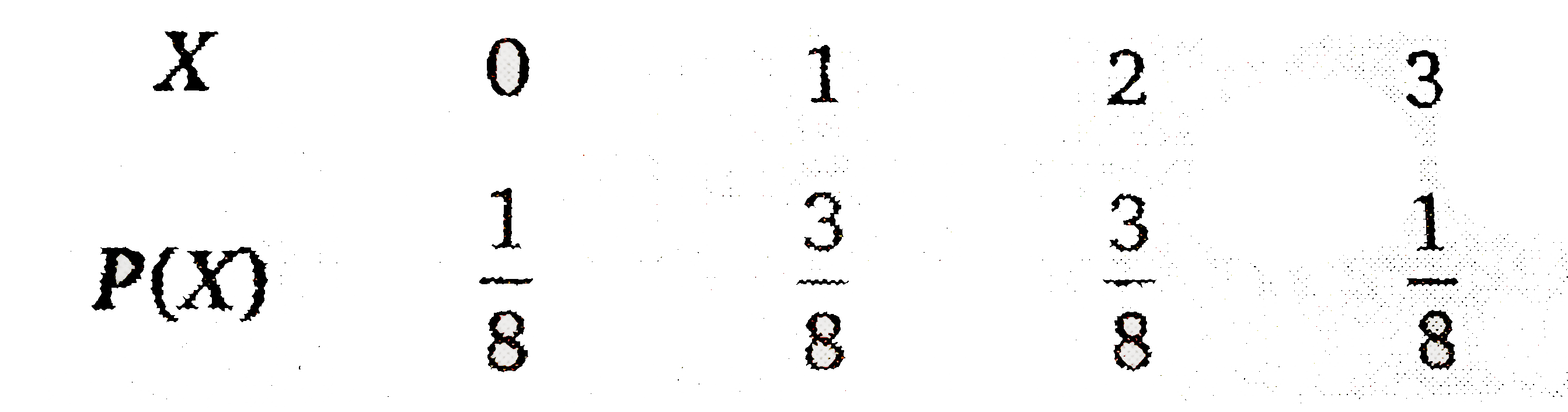
Therefore mean
$= \sum X P (X) = 0 \times \frac{1}{8} + 1 \times \frac{3}{8} + 2 \times \frac{3}{8} + 3 \times \frac{1}{8}$
$= \frac{3}{8} + \frac{6}{8} + \frac{3}{8} = \frac{12}{8} = \frac{3}{2} = 1.5$

|

Updated on:21/07/2023

Class 12 MATHS PROBABILITY

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-PROBABIILITY-Exercise 13.4

Home
Ask Doubt
Profile