Find the mean of the following frequency distribution, using step-deviation method: Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 12 13 10 8
To find the mean of the given frequency distribution using the step-deviation method, we will follow these steps:
Step 1: Prepare the Data
We have the following class intervals and their corresponding frequencies:
| Class Interval | Frequency (f) |
|----------------|---------------|
| 0 - 10 | 7 |
| 10 - 20 | 12 |
| 20 - 30 | 13 |
| 30 - 40 | 10 |
| 40 - 50 | 8 |
Step 2: Calculate the Midpoint (xi)
The midpoint (xi) for each class interval is calculated as follows:
- For 0 - 10: x1=0+102=5
- For 10 - 20: x2=10+202=15
- For 20 - 30: x3=20+302=25
- For 30 - 40: x4=30+402=35
- For 40 - 50: x5=40+502=45
| Class Interval | Frequency (f) | Midpoint (xi) |
|----------------|---------------|----------------|
| 0 - 10 | 7 | 5 |
| 10 - 20 | 12 | 15 |
| 20 - 30 | 13 | 25 |
| 30 - 40 | 10 | 35 |
| 40 - 50 | 8 | 45 |
Step 3: Choose an Assumed Mean (a)
Let's assume the mean (a) to be 25 (which is the midpoint of the distribution).
Step 4: Calculate the Deviation (di)
The deviation (di) is calculated as di=xi−a:
| Midpoint (xi) | Deviation (di) |
|----------------|----------------|
| 5 | 5 - 25 = -20 |
| 15 | 15 - 25 = -10 |
| 25 | 25 - 25 = 0 |
| 35 | 35 - 25 = 10 |
| 45 | 45 - 25 = 20 |
Step 5: Calculate the Step Deviation (ui)
The step deviation (ui) is calculated as ui=dih, where h is the class width (10).
| Deviation (di) | Step Deviation (ui) |
|----------------|----------------------|
| -20 | -20 / 10 = -2 |
| -10 | -10 / 10 = -1 |
| 0 | 0 / 10 = 0 |
| 10 | 10 / 10 = 1 |
| 20 | 20 / 10 = 2 |
Step 6: Calculate fi⋅ui
Now, we calculate fi⋅ui:
| Frequency (f) | Step Deviation (ui) | fi⋅ui |
|----------------|----------------------|--------------------|
| 7 | -2 | 7 * -2 = -14 |
| 12 | -1 | 12 * -1 = -12 |
| 13 | 0 | 13 * 0 = 0 |
| 10 | 1 | 10 * 1 = 10 |
| 8 | 2 | 8 * 2 = 16 |
Step 7: Calculate Summation
Now, we calculate the summation of frequencies and fi⋅ui:
- Σf=7+12+13+10+8=50
- Σ(fi⋅ui)=−14−12+0+10+16=0
Step 8: Calculate the Mean
Using the formula for the mean:
¯x=a+Σ(fi⋅ui)Σf⋅h
Substituting the values:
¯x=25+050⋅10=25+0=25
Final Answer
The mean of the frequency distribution is 25.
---
We have the following class intervals and their corresponding frequencies:
|----------------|---------------|
| 0 - 10 | 7 |
| 10 - 20 | 12 |
| 20 - 30 | 13 |
| 30 - 40 | 10 |
| 40 - 50 | 8 |
The midpoint (xi) for each class interval is calculated as follows:
- For 10 - 20: x2=10+202=15
- For 20 - 30: x3=20+302=25
- For 30 - 40: x4=30+402=35
- For 40 - 50: x5=40+502=45
|----------------|---------------|----------------|
| 0 - 10 | 7 | 5 |
| 10 - 20 | 12 | 15 |
| 20 - 30 | 13 | 25 |
| 30 - 40 | 10 | 35 |
| 40 - 50 | 8 | 45 |
Let's assume the mean (a) to be 25 (which is the midpoint of the distribution).
The deviation (di) is calculated as di=xi−a:
|----------------|----------------|
| 5 | 5 - 25 = -20 |
| 15 | 15 - 25 = -10 |
| 25 | 25 - 25 = 0 |
| 35 | 35 - 25 = 10 |
| 45 | 45 - 25 = 20 |
The step deviation (ui) is calculated as ui=dih, where h is the class width (10).
|----------------|----------------------|
| -20 | -20 / 10 = -2 |
| -10 | -10 / 10 = -1 |
| 0 | 0 / 10 = 0 |
| 10 | 10 / 10 = 1 |
| 20 | 20 / 10 = 2 |
Now, we calculate fi⋅ui:
|----------------|----------------------|--------------------|
| 7 | -2 | 7 * -2 = -14 |
| 12 | -1 | 12 * -1 = -12 |
| 13 | 0 | 13 * 0 = 0 |
| 10 | 1 | 10 * 1 = 10 |
| 8 | 2 | 8 * 2 = 16 |
Now, we calculate the summation of frequencies and fi⋅ui:
- Σ(fi⋅ui)=−14−12+0+10+16=0
Using the formula for the mean:
The mean of the frequency distribution is 25.
Topper's Solved these Questions
Similar Questions
Find the mean of the following frequency distribution using step-deviation method. Class 0-10 10-20 20-30 30-40 40-50 Frequency 7 10 15 8 10
View SolutionFind the mean of the following distribution: 10 30 50 70 89 7 8 10 15 10
View SolutionFind the mean of the following distribution: x: 10 30 50 70 89 f: 7 8 10 15 10
View SolutionFind the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View SolutionFind the mean of the following frequency distributions: Class interval: 0-6 6-12 12-18 18-24 24-30 Frequency: 7 5 10 12 6
View SolutionFind the mean of the following frequency distributions: Classinterval: 0−8 8−16 16−24 24−32 32−40 Frequency: 5 9 10 8 8
View SolutionFind the mean of the following frequency distributions: Class interval: 0-6 6-12 12-18 18-24 24-30 Frequency: 6 8 10 9 7
View SolutionFind the mean of the following frequency distributions: Class interval: 0-8 8-16 16-24 24-32 32-40 Frequency: 6 7 10 8 9
View SolutionFind the mean of the following frequency distribution: Class-interval: 0-10 10-20 20-30 30-40 40-50 No. of workers f: 7 10 15 8 10
View SolutionConsider the following distribution
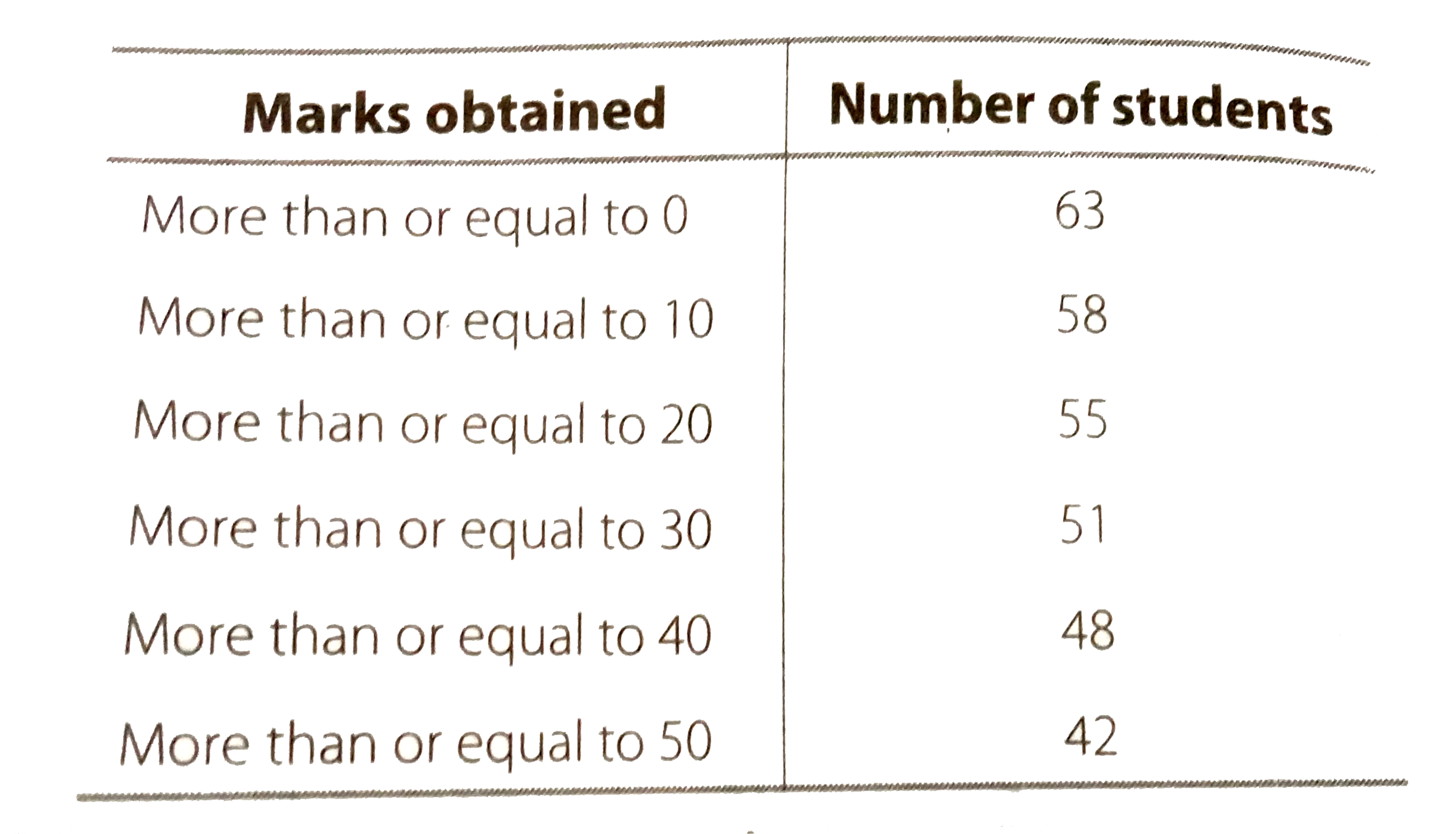
Frequency of the class 30-40 isView Solution

