Find the mean of the following frequency distributions: Class interval: 25-35 35-45 45-55 55-65 65-75 Frequency: 6 10 8 12 4
To find the mean of the given frequency distribution, we will follow these steps:
Step 1: Identify the Class Intervals and Frequencies
We have the following class intervals and their corresponding frequencies:
- Class Intervals: 25-35, 35-45, 45-55, 55-65, 65-75
- Frequencies: 6, 10, 8, 12, 4
Step 2: Calculate the Class Marks
The class mark (midpoint) for each class interval can be calculated using the formula:
Class Mark=Lower Limit+Upper Limit2
Calculating the class marks:
- For 25-35: 25+352=30
- For 35-45: 35+452=40
- For 45-55: 45+552=50
- For 55-65: 55+652=60
- For 65-75: 65+752=70
So the class marks are: 30, 40, 50, 60, 70.
Step 3: Calculate fi×xi
Now, we will multiply each frequency by its corresponding class mark:
- 6×30=180
- 10×40=400
- 8×50=400
- 12×60=720
- 4×70=280
Now we can summarize this in a table:
| Class Interval | Frequency (fi) | Class Mark (xi) | fi×xi |
|----------------|-----------------------|------------------------|-----------------------|
| 25-35 | 6 | 30 | 180 |
| 35-45 | 10 | 40 | 400 |
| 45-55 | 8 | 50 | 400 |
| 55-65 | 12 | 60 | 720 |
| 65-75 | 4 | 70 | 280 |
| Total | 40 | | 1980 |
Step 4: Calculate the Total Frequencies and Total of fi×xi
- Total frequency Σfi=6+10+8+12+4=40
- Total of fi×xi=180+400+400+720+280=1980
Step 5: Calculate the Mean
The mean (¯x) can be calculated using the formula:
¯x=ΣfixiΣfi
Substituting the values:
¯x=198040=49.5
Conclusion
The mean of the given frequency distribution is 49.5.
---
We have the following class intervals and their corresponding frequencies:
- Class Intervals: 25-35, 35-45, 45-55, 55-65, 65-75
- Frequencies: 6, 10, 8, 12, 4
The class mark (midpoint) for each class interval can be calculated using the formula:
Class Mark=Lower Limit+Upper Limit2
- For 25-35: 25+352=30
- For 35-45: 35+452=40
- For 45-55: 45+552=50
- For 55-65: 55+652=60
- For 65-75: 65+752=70
Now, we will multiply each frequency by its corresponding class mark:
- 6×30=180
- 10×40=400
- 8×50=400
- 12×60=720
- 4×70=280
|----------------|-----------------------|------------------------|-----------------------|
| 25-35 | 6 | 30 | 180 |
| 35-45 | 10 | 40 | 400 |
| 45-55 | 8 | 50 | 400 |
| 55-65 | 12 | 60 | 720 |
| 65-75 | 4 | 70 | 280 |
| Total | 40 | | 1980 |
- Total frequency Σfi=6+10+8+12+4=40
- Total of fi×xi=180+400+400+720+280=1980
The mean (¯x) can be calculated using the formula:
¯x=ΣfixiΣfi
¯x=198040=49.5
The mean of the given frequency distribution is 49.5.
Topper's Solved these Questions
Similar Questions
Find the mean for the following frequency distribution :
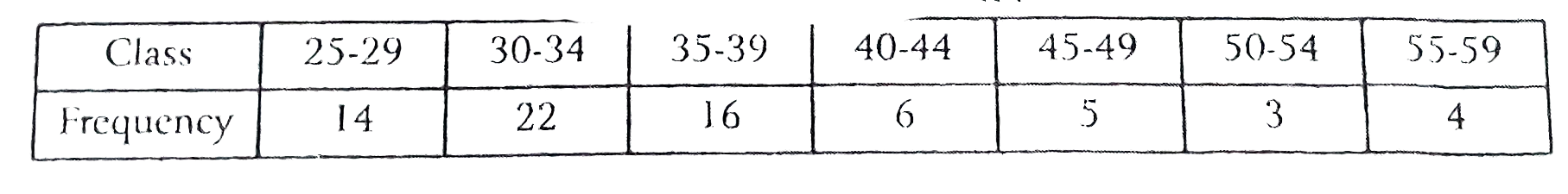 View Solution
View SolutionFind the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View SolutionFind the mean of the following frequency distributions: Classinterval: 0−8 8−16 16−24 24−32 32−40 Frequency: 5 6 4 3 2
View SolutionFind the mean of the following frequency distributions: Classinterval: 0−8 8−16 16−24 24−32 32−40 Frequency: 5 9 10 8 8
View SolutionFind the mean of the following frequency distributions: Class interval: 0-6 6-12 12-18 18-24 24-30 Frequency: 6 8 10 9 7
View SolutionFind the mean of the following frequency distributions: Class interval: 0-6 6-12 12-18 18-24 24-30 Frequency: 7 5 10 12 6
View SolutionFind the mean of the following frequency distributions: Class interval: 0-8 8-16 16-24 24-32 32-40 Frequency: 6 7 10 8 9
View SolutionFind the mean of the following frequency distributions: Classinterval: 10−30 30−50 50−70 70−90 90−110 110−130 Frequency: 5 8 12 20 3 2
View SolutionFind the mean of the following frequency distribution: Class-interval: 0-10 10-20 20-30 30-40 40-50 No. of workers f: 7 10 15 8 10
View SolutionWrite the modal class for the following frequency distribution: Class-interval: 10-15 15-20 20-25 25-30 30-35 35-40 Frequency: 30 35 75 40 30 15
View Solution

