Find the median of the following data: 41, 43, 127, 99, 61, 92, 71, 58, 57 if 58 is replaced by 85, what will be the new median.
To find the median of the given data set, we will follow these steps:
Step 1: Arrange the Data in Ascending Order
The given data is: 41, 43, 127, 99, 61, 92, 71, 58, 57.
First, we need to arrange this data in ascending order:
- The smallest number is 41.
- Next is 43.
- Then comes 57.
- Followed by 58.
- Next is 61.
- Then 71.
- Next is 92.
- Followed by 99.
- Finally, the largest number is 127.
So, the arranged data in ascending order is:
41, 43, 57, 58, 61, 71, 92, 99, 127.
Step 2: Count the Number of Observations
Now, we count the number of observations in the data set:
- There are 9 observations.
Step 3: Determine the Median Position
Since the number of observations (n) is odd (n = 9), the median is found at the position given by the formula:
Median Position=n+12=9+12=102=5.
This means the median is the 5th observation in the ordered data.
Step 4: Find the Median
Now, we look for the 5th observation in our arranged data:
1. 1st: 41
2. 2nd: 43
3. 3rd: 57
4. 4th: 58
5. 5th: 61
Thus, the median of the original data set is 61.
Step 5: Replace 58 with 85 and Re-arrange
Next, we replace 58 with 85 in the original data set:
- The new data set becomes: 41, 43, 127, 99, 61, 92, 71, 85, 57.
Now, we arrange this new data in ascending order:
- The smallest number is still 41.
- Next is 43.
- Then comes 57.
- Followed by 61.
- Next is 71.
- Then 85 (since we replaced 58 with 85).
- Next is 92.
- Followed by 99.
- Finally, the largest number is 127.
So, the new arranged data in ascending order is:
41, 43, 57, 61, 71, 85, 92, 99, 127.
Step 6: Count the Number of Observations Again
The number of observations remains the same at 9.
Step 7: Determine the New Median Position
Again, since the number of observations is odd (n = 9), the median is still at the position:
Median Position=n+12=9+12=102=5.
Step 8: Find the New Median
Now, we look for the 5th observation in the newly arranged data:
1. 1st: 41
2. 2nd: 43
3. 3rd: 57
4. 4th: 61
5. 5th: 71
Thus, the new median after replacing 58 with 85 is 71.
Summary of Results
- The median of the original data set is 61.
- The new median after replacing 58 with 85 is 71.
The given data is: 41, 43, 127, 99, 61, 92, 71, 58, 57.
- The smallest number is 41.
- Next is 43.
- Then comes 57.
- Followed by 58.
- Next is 61.
- Then 71.
- Next is 92.
- Followed by 99.
- Finally, the largest number is 127.
41, 43, 57, 58, 61, 71, 92, 99, 127.
Now, we count the number of observations in the data set:
- There are 9 observations.
Since the number of observations (n) is odd (n = 9), the median is found at the position given by the formula:
Median Position=n+12=9+12=102=5.
This means the median is the 5th observation in the ordered data.
Now, we look for the 5th observation in our arranged data:
1. 1st: 41
2. 2nd: 43
3. 3rd: 57
4. 4th: 58
5. 5th: 61
Next, we replace 58 with 85 in the original data set:
- The new data set becomes: 41, 43, 127, 99, 61, 92, 71, 85, 57.
- The smallest number is still 41.
- Next is 43.
- Then comes 57.
- Followed by 61.
- Next is 71.
- Then 85 (since we replaced 58 with 85).
- Next is 92.
- Followed by 99.
- Finally, the largest number is 127.
41, 43, 57, 61, 71, 85, 92, 99, 127.
The number of observations remains the same at 9.
Again, since the number of observations is odd (n = 9), the median is still at the position:
Median Position=n+12=9+12=102=5.
Now, we look for the 5th observation in the newly arranged data:
1. 1st: 41
2. 2nd: 43
3. 3rd: 57
4. 4th: 61
5. 5th: 71
- The median of the original data set is 61.
- The new median after replacing 58 with 85 is 71.
Topper's Solved these Questions
Similar Questions
Find the median of the following data 41, 43, 127, 99, 71, 92, 71, 58, 57
View SolutionFind the median for the following data :
 View Solution
View SolutionFind the median for the following data :
 View Solution
View SolutionFind the median from the following data :
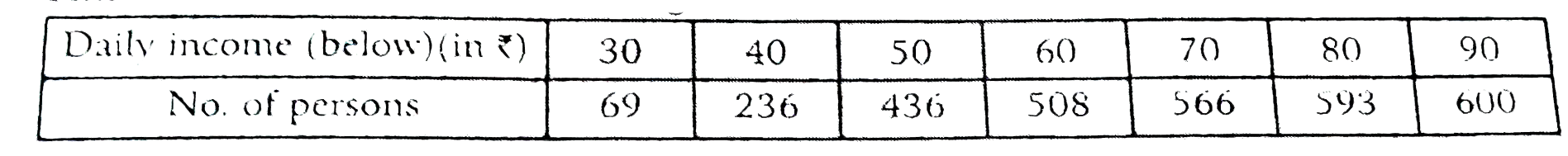 View Solution
View SolutionFind the median from the following data :
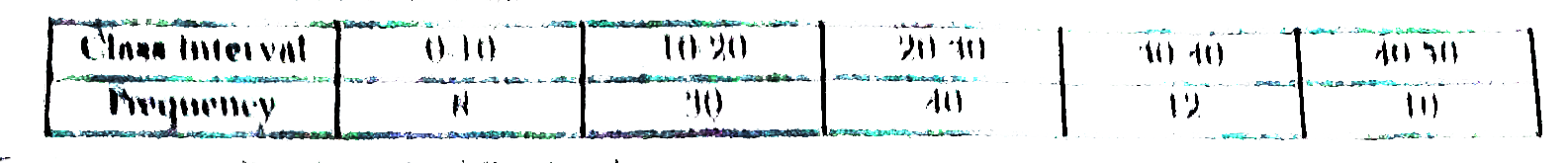 View Solution
View SolutionFind the median from the following data :
 View Solution
View SolutionFind the median for the following data
 View Solution
View SolutionFind the median of the following data: 19, 25, 59, 48, 35, 31, 30, 32, 51.
If 25 is replaced by 52, what will be the new median.View SolutionFind the median of the following data 31, 38, 27, 28, 36, 25, 35, 40
View SolutionFind the median of the following data 15, 6, 16, 8, 22, 21, 9, 18, 25
View Solution

