Find the median of the following data: class : 0−10,equency:5, 10−20,3, 20−30,4, 30−40,3, 40−50,3,50-60 , 4,60-70 , 7, 70-80 , 9,80-90 , 7,90-100 , 8,
To find the median of the given frequency distribution, we will follow these steps:
Step 1: Organize the Data
We start by organizing the given data into a table format, which includes the class intervals and their corresponding frequencies.
| Class Interval | Frequency |
|----------------|-----------|
| 0 - 10 | 5 |
| 10 - 20 | 3 |
| 20 - 30 | 4 |
| 30 - 40 | 3 |
| 40 - 50 | 3 |
| 50 - 60 | 4 |
| 60 - 70 | 7 |
| 70 - 80 | 9 |
| 80 - 90 | 7 |
| 90 - 100 | 8 |
Step 2: Calculate Cumulative Frequency
Next, we calculate the cumulative frequency for the data. This is done by adding the frequency of each class to the cumulative frequency of the previous class.
| Class Interval | Frequency | Cumulative Frequency |
|----------------|-----------|----------------------|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 3 | 8 |
| 20 - 30 | 4 | 12 |
| 30 - 40 | 3 | 15 |
| 40 - 50 | 3 | 18 |
| 50 - 60 | 4 | 22 |
| 60 - 70 | 7 | 29 |
| 70 - 80 | 9 | 38 |
| 80 - 90 | 7 | 45 |
| 90 - 100 | 8 | 53 |
Step 3: Determine Total Frequency (N)
The total frequency (N) is the last cumulative frequency value, which is 53.
Step 4: Calculate N/2
Now, we calculate N/2:
N/2=53/2=26.5
Step 5: Identify the Median Class
The median class is the class interval where the cumulative frequency is just greater than N/2. From our cumulative frequency table, we see that the cumulative frequency of 29 (for the class 60-70) is the first to exceed 26.5. Thus, the median class is 60-70.
Step 6: Define the Median Class Parameters
For the median class (60-70):
- Lower limit (L) = 60
- Frequency (f) = 7 (frequency of the median class)
- Cumulative frequency (Cf) = 22 (cumulative frequency of the class before the median class)
- Class width (H) = 10 (difference between upper and lower limits of the median class)
Step 7: Apply the Median Formula
The formula for the median in a grouped frequency distribution is:
Median=L+(N/2−Cff)×H
Substituting the values:
Median=60+(26.5−227)×10
Step 8: Calculate the Median
First, calculate N/2−Cf:
26.5−22=4.5
Now substitute this back into the formula:
Median=60+(4.57)×10
=60+(0.642857)×10
=60+6.42857
=66.42857
Rounding to two decimal places, the median is approximately:
Median≈66.43
Final Answer
The median of the given data is approximately 66.43.
---
We start by organizing the given data into a table format, which includes the class intervals and their corresponding frequencies.
|----------------|-----------|
| 0 - 10 | 5 |
| 10 - 20 | 3 |
| 20 - 30 | 4 |
| 30 - 40 | 3 |
| 40 - 50 | 3 |
| 50 - 60 | 4 |
| 60 - 70 | 7 |
| 70 - 80 | 9 |
| 80 - 90 | 7 |
| 90 - 100 | 8 |
Next, we calculate the cumulative frequency for the data. This is done by adding the frequency of each class to the cumulative frequency of the previous class.
|----------------|-----------|----------------------|
| 0 - 10 | 5 | 5 |
| 10 - 20 | 3 | 8 |
| 20 - 30 | 4 | 12 |
| 30 - 40 | 3 | 15 |
| 40 - 50 | 3 | 18 |
| 50 - 60 | 4 | 22 |
| 60 - 70 | 7 | 29 |
| 70 - 80 | 9 | 38 |
| 80 - 90 | 7 | 45 |
| 90 - 100 | 8 | 53 |
The total frequency (N) is the last cumulative frequency value, which is 53.
Now, we calculate N/2:
N/2=53/2=26.5
The median class is the class interval where the cumulative frequency is just greater than N/2. From our cumulative frequency table, we see that the cumulative frequency of 29 (for the class 60-70) is the first to exceed 26.5. Thus, the median class is 60-70.
For the median class (60-70):
- Lower limit (L) = 60
- Frequency (f) = 7 (frequency of the median class)
- Cumulative frequency (Cf) = 22 (cumulative frequency of the class before the median class)
- Class width (H) = 10 (difference between upper and lower limits of the median class)
The formula for the median in a grouped frequency distribution is:
Median=L+(N/2−Cff)×H
Median=60+(26.5−227)×10
First, calculate N/2−Cf:
26.5−22=4.5
Median=60+(4.57)×10
=60+(0.642857)×10
=60+6.42857
=66.42857
Median≈66.43
The median of the given data is approximately 66.43.
Topper's Solved these Questions
Similar Questions
Find the mean and median of the data is 10 , 15 , 17 , 19 , 20 and 21 .
View SolutionFind the mean of the following frequency distributions: Class interval: 0-10 10-20 20-30 30-40 40-50 Frequency: 9 12 15 10 14
View SolutionFind the median of the following data:
Class Interval0−1010−2020−3030−4040−50f68547View SolutionWrite the median class of the following distribution: Classes: 0-10 10-20 20-30 30-40 40-50 50-60 60-70 Frequency: 4 4 8 10 12 8 4
View SolutionFind out median of the following series :
Size152025303540Frequency1015255520View SolutionFind the mean of the following frequency distributions: Class interval: 10-30 30-50 50-70 70-90 90-110 110-130 Frequency: 5 8 12 20 3 2
View SolutionCalculate the median from the following distribution: Class: 5-10 10-15 15-20 20-25 25-30 30-35 35-40 40-45 Frequency: 5 6 15 10 5 4 2 2
View SolutionFind the mean of the following frequency distribution: Class-interval: 0-10 10-20 20-30 30-40 40-50 No. of workers f: 7 10 15 8 10
View SolutionFind the mean deviation about median for the following data
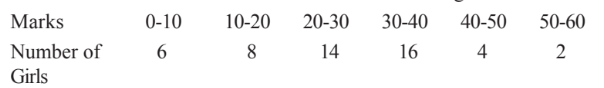 View Solution
View SolutionIf the mean of the following distribution is 27, find the value of p . Class: 0-10 10-20 20-30 30-40 40-50 Frequency: 8 p 12 13 10
View Solution

