Find the point (α,)β on the ellipse 4x2+3y2=12, in the first quadrant, so that the area enclosed by the lines y=x,y=β,x=α , and the x-axis is maximum.
Video Solution
Text Solution
The correct Answer is:(3/2,1)
The equation of the ellipse is x23+y24=1
Let point P be (√3cos,θ,2sinθ),θ∈(0,π/2)
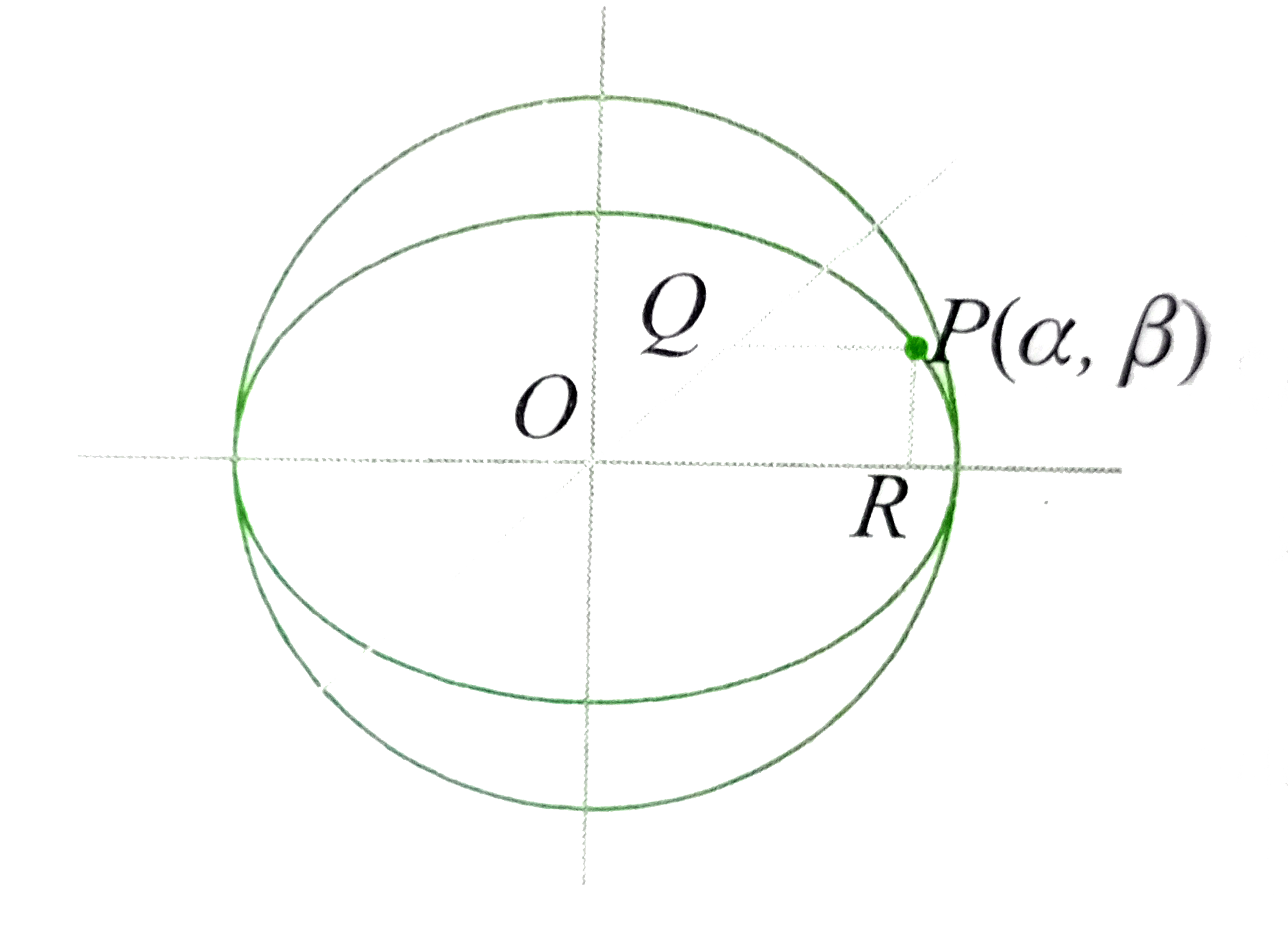
Clearly, line PQ is y=sinθ , line PR is x=√3cosθ, line OQ is y=x, and Q is (2sinθ,2sinθ),
Z= Area of region PQORP (tranpezium)
=12(OR+PQ)PR
=12(√3cosθ+√3cosθ−2sinθ)2sinθ
=(2√3cosθsinθ−2sin2θ)
=(√3sin2θ+cos2θ−1)
=2cosθ(2θ−π3)−1
which is maximum when cos(θ−π3) is maximum
∴2θ−π3=0
or θ=π6
Hence, point P is (3/2,1)
|
Similar Questions
Knowledge Check
The line 2y=3x+12 cuts the parabola 4y=3x2
What is the area enclosed by the parabola, the line and the y-axis in the first quadrant?A7 square unitB14 square unitC20 square unitD21 square unitThe area in the positive quadrant enclosed by the circle x2+y2=4, the line x=y√3 and X-axis is
Aπ2Bπ4Cπ3DπFind the area of region in the first quadrant enclosed the X-axis, the line y =x and the circlex2+y2=32.
A4π sq unitsB3π sq unitsC5π sq unitsDNone of these
Find the area enclosed in the first quadrant by x2+y2=9
View SolutionFind the area of the region bouonded by y2=4x,x=1,x=4 and x-axis in the first quadrant.
View SolutionFind the area of the region in the first quadrant enclosed by the x-axis, the line y=x and the circle x2+y2=32.
View SolutionFind the area bounded by the curve 2x2−y=0 and the lines x=3,y=1 and the x-axis all in first quadrant.
View SolutionFind the area of the region in the first quadrant enclosed by the x-axis, the line y=x, and the circle x2+y2=32.
View Solution
