Question

Find the probability distribution of
(i) number
of heads in two tosses of a coin.
(ii) number
of tails in the simultaneous tosses of three corns.
(iii) number
of heads in four tosses of a com.

Answer

N/a

Explanation

(i) Sample space in two throws of a coin is
`S={HH,HT,TH,"TT"}`
Let `X` represnets the number of heads for the sample space `S`.
`X("HH")=2,X(HT)=1,X(TH)=1` and `X("TT")-0`
Therefore possible values of random variable `X` are 0,1, or 2.
We know that
`P("HH")=P(HT)=P(TH)=P("TT")=1/4`
`:.P(X=0)=P` (getting tail on two throws)
`=P({"TT"})=1/4`
`P(X=1)=P` (getting one head and one tail)
`=P({TH,HT})=2/4=1/2`
and `P(X)=2)=P` (getting heads on two throws)
`=P({"HHH})=1/4`
Therefore required probability distribution for `X` is

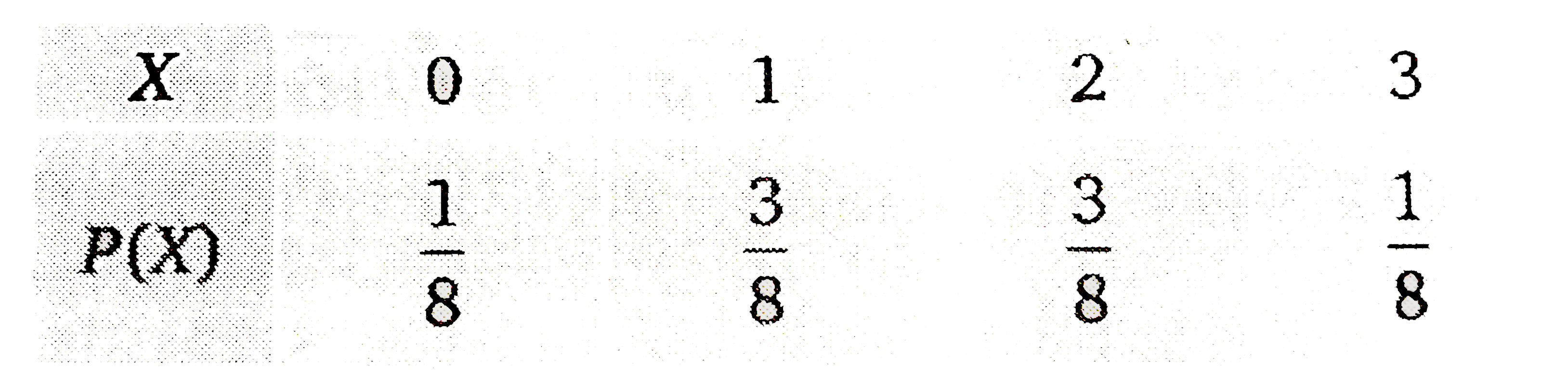
(ii) Sample space in one throw of three coins is
`S={"HHH,HHT,HTH,HTT,THH,THT,TTH,TTt"}`
`implies n(S)=8`
Let `X` represents the number of tails.
Therefore the possible values of random variable `X` are 0,1,2 and 3.
`P(X=0)=P` (no tail) `=P({"HHH"})=1/8`
`P(X=1)=P` (on getting one tail and two heads)
`=P({"HHT,HTH,THH})=3/8`
`P(X=2)=P` (getting two tails and one head)
`=P({"HTT,THT,TTH"})=3/8`
and `P(X=3)=P` (getting three heads)
`=P({"TTT"})=1/8`
Therefore, the required probability distribution for `X` is:

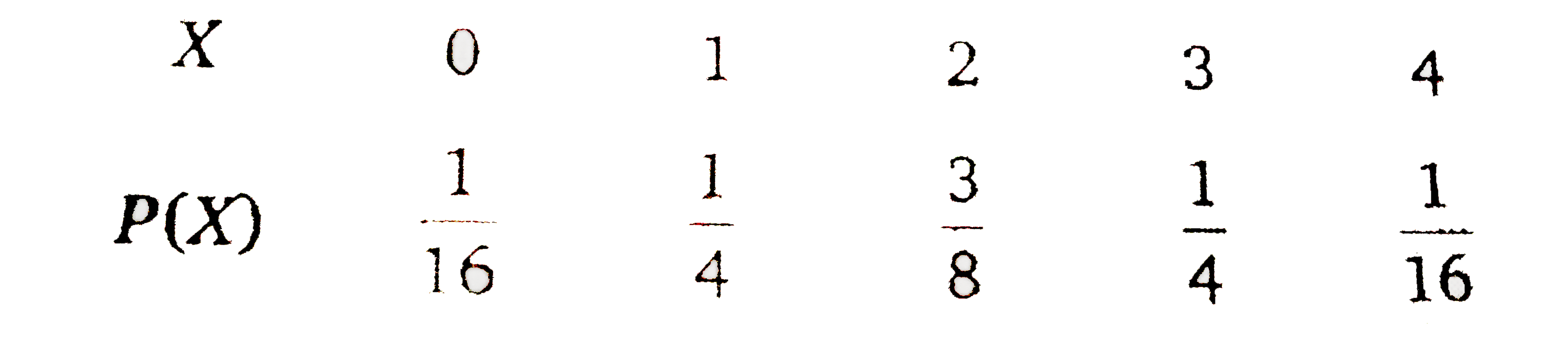
(ii) Sample space in four throws of a coin is
`S={{:(HHHH","HHHT","HHTH","HTHT","H"TT"H","H"TTT"),("THHH,HTHH,TTHT"),("THHT,THTH,HHTT,TTHH,TTHH,THTT,TTT"):}}`
`implies n(S)=16`
Let `X` is a random variable which represents the number of heads obtained whose possible values are 0,1,2,3 or 4.
`P(X=0)=P` (getting no head)
`=P({"TTTT"})=1/16`
`P(X=1)=P` (getting one head and three tails)
`=P({"HTTT,THTT,TTHT,TTHT"})`
`=4/16=1/4`
`P(X=2)=P` (getting two heads adn two tails)
`=P{"HHTT,HTHT,HTTH,THHT,THTH,TTHH"})`
`=6/16=3/8`
`P(X=3)-P` (getting three heads and one tail)
`=P({"HHHT,HHTH,HTHH,THHH"})=4/16=1/4`
and `P(X=4)=P` (getting four heads)
`=P({"HHHH"})=1/16`
Therefore the required probability distribution is,