Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter Z as Z
The correct Answer is:3n
To find the rule that gives the number of matchsticks required to make the letter "Z", we can follow these steps:
Step 1: Identify the number of matchsticks for one "Z"
To create the letter "Z" using matchsticks, we can visualize it as follows:
- The top horizontal line requires 1 matchstick.
- The diagonal line requires 1 matchstick.
- The bottom horizontal line requires 1 matchstick.
So, the total number of matchsticks needed to form one "Z" is:
1+1+1=3
Step 2: Establish a variable for the number of "Z"s
Let’s denote the number of "Z"s we want to create as n.
Step 3: Write the rule using the variable
Since each "Z" requires 3 matchsticks, if we want to create n "Z"s, the total number of matchsticks required can be expressed as:
Total matchsticks=3n
Step 4: Verify the rule with examples
- If n=1 (1 "Z"):
3×1=3 matchsticks
- If n=2 (2 "Z"s):
3×2=6 matchsticks
- If n=3 (3 "Z"s):
3×3=9 matchsticks
- If n=4 (4 "Z"s):
3×4=12 matchsticks
Conclusion
The rule for the number of matchsticks required to create n letters "Z" is:
Total matchsticks=3n
To create the letter "Z" using matchsticks, we can visualize it as follows:
- The top horizontal line requires 1 matchstick.
- The diagonal line requires 1 matchstick.
- The bottom horizontal line requires 1 matchstick.
1+1+1=3
Let’s denote the number of "Z"s we want to create as n.
Since each "Z" requires 3 matchsticks, if we want to create n "Z"s, the total number of matchsticks required can be expressed as:
Total matchsticks=3n
- If n=1 (1 "Z"):
3×1=3 matchsticks
- If n=2 (2 "Z"s):
3×2=6 matchsticks
- If n=3 (3 "Z"s):
3×3=9 matchsticks
- If n=4 (4 "Z"s):
3×4=12 matchsticks
The rule for the number of matchsticks required to create n letters "Z" is:
Total matchsticks=3n
Topper's Solved these Questions
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.2)
5 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - NCERT SECTION (EXERCISE - 11.3)
24 Videos
- ALGEBRABOOK - MTG IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - SOLVED EXAMPLES
24 Videos
- BASIC GEOMETRICAL IDEASBOOK - MTG IIT JEE FOUNDATIONCHAPTER - BASIC GEOMETRICAL IDEASEXERCISE - OLYMPIAD/HOTS CORNER
10 Videos
Similar Questions
Find the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter T as T
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter U as U
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter V as V
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter E as E
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter S as S
View SolutionFind the rule which gives the number of matchsticks required to make the following matchstick patterns. Use a variable to write the rule.
A pattern of letter A as A
View SolutionFind the rule which gives the number of matchsticks required to make thefollowing matchstick patterns. Use a variable to write the rule.(a) A pattern of letter T as(b) A pattern of letter Z as(c) A pattern of letter U as(d) A pattern of letter V as(e) A pattern of letter E as(f) A pattern of letter S as(g) A pattern of letter A as
View SolutionFind the number of matchsticks used in nth pattern.
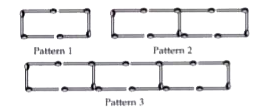
View SolutionFind the number of dots in the pattern 143 of the following pattern.

View SolutionFind the pattern followed in given figure and the number of matchsticks used in 86th figure.
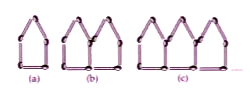
View Solution
