Find the smallest number greater than 2 which gives a remainder 2 when divided by 16,18 and 24.
Video Solution
Text Solution
The correct Answer is:146
The requird number is the least common multiples of (16,18,24)+2.
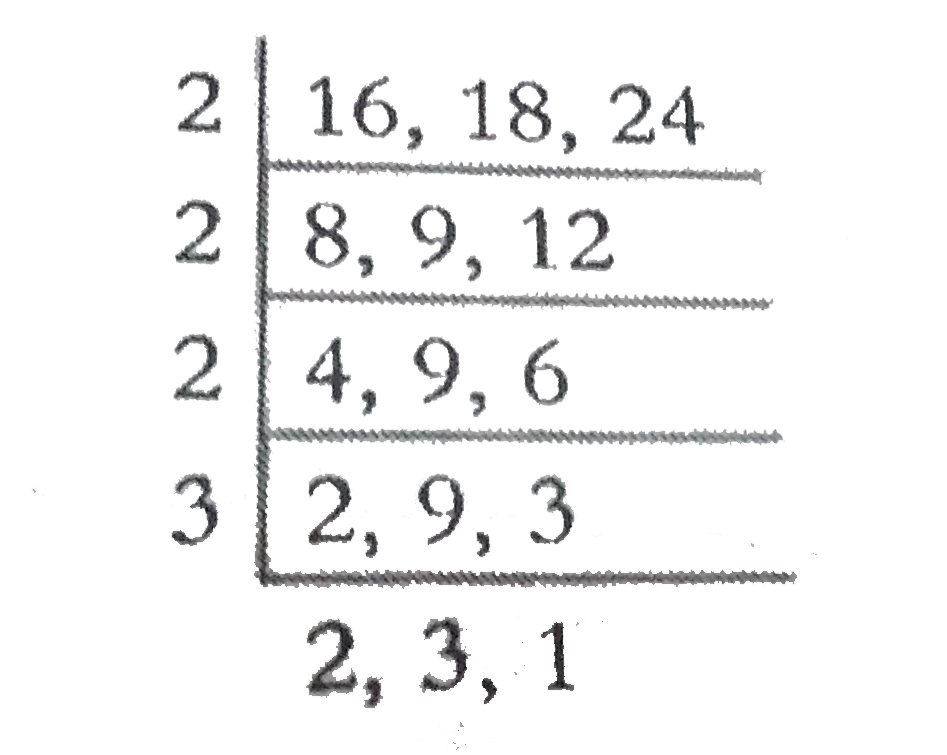
LCM=2×2×2×3×2×3=144
∴ The required number is 144+2=146
|
Topper's Solved these Questions
- FACTORS AND MULTIPLES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FACTORS AND MULTIPLES EXERCISE - Concept Application
5 Videos
- FACTORS AND MULTIPLES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FACTORS AND MULTIPLES EXERCISE - Assessment Test
15 Videos
- FACTORS AND MULTIPLES BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FACTORS AND MULTIPLES EXERCISE - Test Your Concepts ( Match the Column ) :
1 Videos
- ALGEBRABOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - ALGEBRAEXERCISE - CROSSWORD
1 Videos
- FRACTIONS AND DECIMALS BOOK - PEARSON IIT JEE FOUNDATIONCHAPTER - FRACTIONS AND DECIMALS EXERCISE - Crossword
1 Videos
Similar Questions
Knowledge Check
Find the smallest number which leave remainder 2, when divided by 6, 9,12, 15 and 18? (a) 180 (b) 182 (c) 178 (d) 176
A180B182C178D176Find the least number which when divided by 12, leaves a remainder 7, when divided by 15, leaves a remainder 10 and when divided by 16, leaves a remainder 11
A115B235C247D475Find the least number greater than 10 which when divided by 15,20 and25 leaves remainder 10 in each case.
A290B300C310D320
Which of the following is the smallest positive integer which gives the remainder 3 when divided with 4,6,8,and10?
View SolutionWhat is the smallest number which leaves remainder 3 when divided by any of the numbers 5, 6 or 8 but leaves no remainder when it is divide by 9 ?
View SolutionWhat is the smallest number which leaves remainder 3 when divided by any of the numbers 5, 6 or 8 but leaves no remainder when it is divide by 9 ?
View SolutionFind the remainder when 518 is divided by 19.
View Solutiona and b are any numbers and x and y are any non negative integers.
l(a) = the greatest integer less than or equal to a
g(a) = the smallest integer greater than or equal to a
r(x,y) = the remainder when x is divided by y.
r(16, 7)-2 is equal to :
View Solution
