Question

Find the square root of $x^2-18x+81$

Explanation

`x -9`

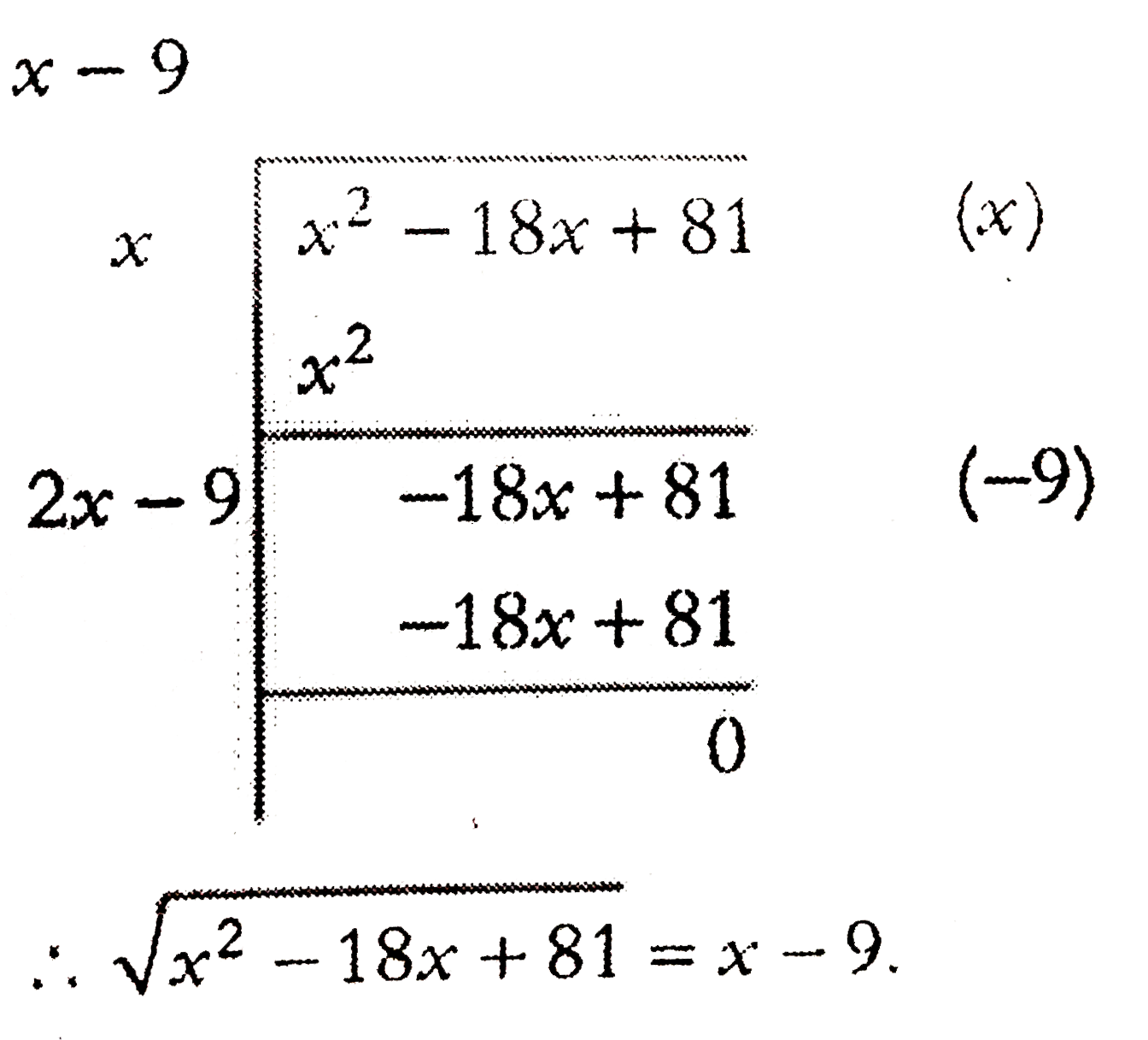
`:. Sqrt(x^(2) - 18x + 81) = x -9`
Step1: First the given expression is arranged in the descending powers of x
Step 2: Then the square root of the first term in the expression is calculated. In the above problem first term is `x^(2)` whose square root is x. This is now the first term of the square root of the expression
Step3: Then the square of x, i.e., `x^(2)` is written below the first term of the expression and subtracted. The difference is zero. Then the next two terms in the expression `- 19x + 81` are brought down as the dividend for the next step. Double the first term of the squre root and put it down as the first term of the next divisor, i.e., `2(x) = 2x` is to be written as the first term of the next divisor. Now the first term `- 18x` of the dividend `- 18x + 81` is to be divided by the first term 2x (of the new divisor). Here we get `-9` which is the second term of the square root of the given expression and the second term of the new divisor.
Step 4: Thus the new divisor becomes `2x -9`. Multiply `(2x -9) " by " (-9)` and the product `-18x + 81` is to be brought down under the second dividend `-18x + 81` and subtracted where we get 0.
Step 5 : Thus `x - 9` is the square root of the given expression `x^(2) - 18x + 81`