Find the sum of the following series up to n terms: (i) 5 + 55 + 555 + . . . (ii) .6 +. 66 +. 666 +. . .
Video Solution
Text Solution
We have,
5+55+555+.. to n terms
=5[1+11+111+…. To n terms]
=59[9+99+999+.. To n terms]
=59[(10−1)+(102−1)+(103−1)+…+(10n−1)]
=59[10×(10n−1)10−1−n]
=59[109(10n−1)−n]
=581[10n+1−10−9n]
(ii) Let
Sn=0.6+0.66+0.666+... to n terms
=6[0.1+0.11+0.111+... to n terms]
=69[0.9+0.99+0.999+.... to n terms]
=69[(1−110)+(1−1102)+(1−1103)+... n terms]
=23[(1+1+...n terms)-110(1+110+1102+..n terms)]
=23⎡⎢
⎢⎣n−110⎛⎜
⎜⎝1−(110)n1−110⎞⎟
⎟⎠⎤⎥
⎥⎦
=23n−23×19(1−10−n)
=23n−227(1−10−n)
|
Topper's Solved these Questions
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ILLUSTRATION 5.53
1 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ILLUSTRATION 5.54
1 Videos
- PROGRESSION AND SERIESBOOK - CENGAGE ENGLISHCHAPTER - PROGRESSION AND SERIESEXERCISE - ILLUSTRATION 5.51
1 Videos
- PROBABILITY IIBOOK - CENGAGE ENGLISHCHAPTER - PROBABILITY IIEXERCISE - MULTIPLE CORRECT ANSWER TYPE
6 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGE ENGLISHCHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Archives (Numerical Value Type)
3 Videos
Similar Questions
Find the sum of the following series whose nth term is: (2n−1)2.
View SolutionFind the sum of the following series whose nth term is: n(n+1)(n+4).
View SolutionFind the sum of the following series up to n terms:(i) 5+55+555+.... (ii) .6+.66+.666+....
View SolutionFind the sum of the series n∑r=1r×r!.
View SolutionFind the cube of 23.
View SolutionFind the cube of 527.
View SolutionFind the sum of the series 313+323++503.
View SolutionFind the sum of the series 313+323++503.
View SolutionComplete the following electron dot diagrams:
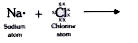
View SolutionComplete the following electron dot diagrams:
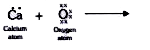
View Solution
