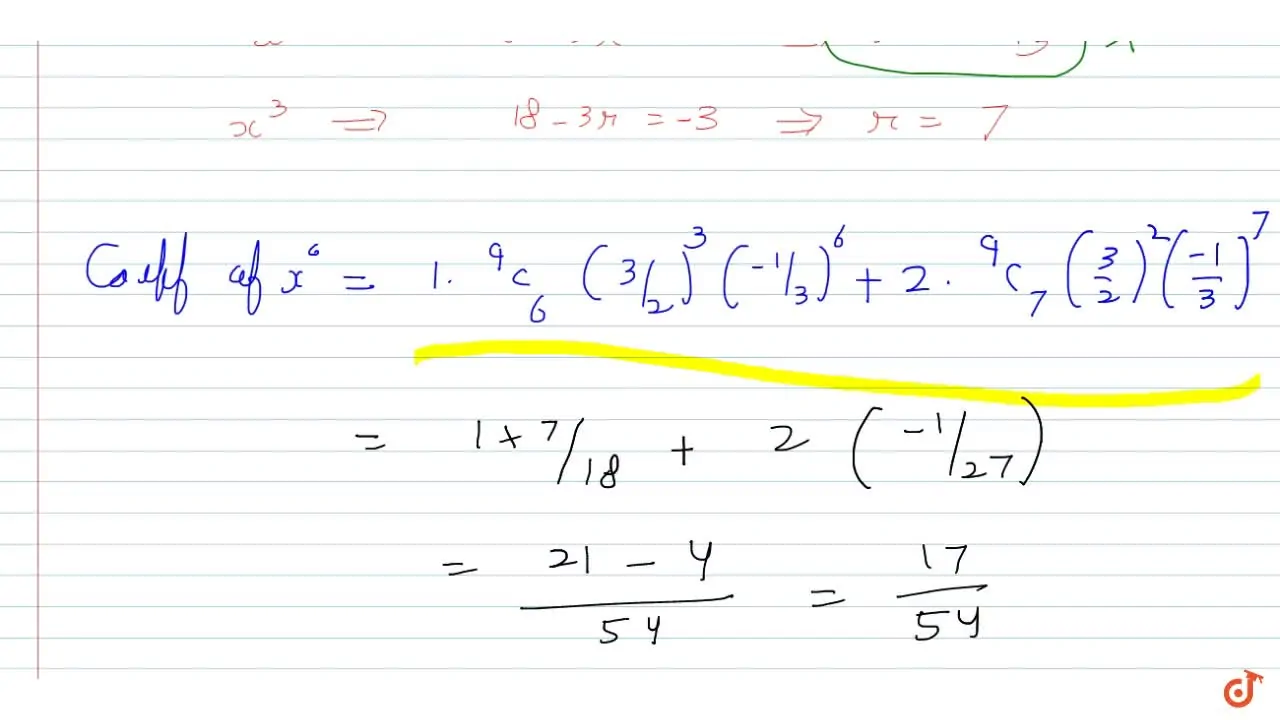Find the term independent of x in the expansion of (1+x+2x3)[(3x2/2)−(1/3)]9
Video Solution
Text Solution
The correct Answer is:1754
In the expansion of E=(32x2−13x)9 , we have
Tr+1=(−1)r⋅9Cr⋅(32x2)(9−r)(13x)r
⇒Tr+1=(−1)r⋅9Cr⋅3(9−2r)2(9−r)⋅x(18−3r).
(1+x+2x3)[(a0×1x3+a1×1x+a2) from E]
=(1+x+2x3)[{(−1)7⋅9C7⋅3−522×1x3}+{(−1)6⋅9C6⋅3−323×x0}]
⎡⎣x=−1⇒18−3r=−1⇒ r is faction18−3r=0⇒r=6and18−3r=−3⇒r=7⎤⎦
=(1+x+2x3)[−127x3+718]
∴ required term (−227+718)=1754.
|
Updated on:21/07/2023
Related Playlists
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - BINOMIAL THEOREMEXERCISE - EXERCISE 10B16videos
BINOMIAL THEOREM
- BOOK - RS AGGARWALCHAPTER - ARITHMETIC PROGRESSIONEXERCISE - Exercise 11F (Very Short-Answer Type Questions)17videos
ARITHMETIC PROGRESSION
- BOOK - RS AGGARWALCHAPTER - CIRCLE EXERCISE - EXERCISE 21 B18videos
CIRCLE
Similar Questions
Find the term independent of x in the expansion of (1+x+2x3)[(3x2/2)−(1/3x)]9
View SolutionFind the term independent of x in the expansion of (2x2−3x3)25
View SolutionFind the term independent of x in the expansion of: (2x2−3x3)10.
View SolutionFind the term independent of x in the expansion (2x2−13x3)10
View SolutionThe term independent of x in the expansion of (2x+13x)6 is
View SolutionFind the term independent of x in the expansion of (3x−2x2)15.
View SolutionFind the term independent of x in the
expansion of (32x2−13x)9View Solutionfind the term independent of 'x' in the expansion of (1+x+2x3)(32x2−13x)9
View SolutionSimplify:- (1700 + 4100 + 5200) / ? = 55
View SolutionThe term independent of x in the expansion of (2x+13x)6 is
View Solution