Find the unit vector along →a−→b where →a=ˆi+3ˆj−ˆk and →b=3ˆi+2ˆj+ˆk.Solution in Tamil
Step by step video & image solution for Find the unit vector along vec a - vec b where veca = hat i + 3 hat j - hat k and vec b = 3 hat i + 2 hat j + hat k. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.3
20 Videos
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.4
7 Videos
- VECTOR ALGEBRABOOK - NEW JOYTHI PUBLICATIONCHAPTER - VECTOR ALGEBRAEXERCISE - ADDITIONAL QUESTIONS FOR PRACTICE 10.1
2 Videos
- TRIGONOMETRIC FUNCTIONSBOOK - NEW JOYTHI PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONSEXERCISE - QUESTIONS FROM COMPETITIVE EXAMS
134 Videos
Similar Questions
Find →a.→b, when →a=ˆi+ˆj+2ˆk and →b=3ˆi+2ˆj−ˆk.
View SolutionShow that the points (1, 2, -1), (2, 5, 1) and (0, -1, -3) are collinear.
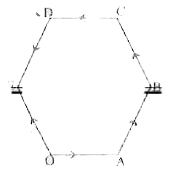
View SolutionIn the figure which vectors are
(i) equal (ii) collinear (iii) coinitial
View SolutionIf A+B+C=90∘ then
cotA+cotB+cotCcotAcotBcotC =
View SolutionLet →a=ˆj−ˆk and →c=ˆi−ˆj−ˆk . Then vector →b satisfying →a×→b+→c=→0 and →a.→b=3 is (1) 2→i−→j+2→k (2) ˆi−ˆj−2ˆk (3) ˆi+j−2ˆk (4) −ˆi+ˆj−2ˆk
View SolutionFind a unit vector perpendicular to both of the vectors →a+→b and →a−→b where →a=ˆi+ˆj+ˆk,→b=ˆi+2ˆj+3ˆk.
View SolutionIf →a=ˆi+ˆj+ˆk, →b=2ˆi−ˆj+3ˆk and →c=ˆi−2ˆj+ˆk find a unit vector parallel to 2→a−→b+3→⋅
View SolutionThe unit vector perpendicular to →A=2ˆi+3ˆj+ˆk and →B=ˆi−ˆj+ˆk is
View SolutionIf →a=ˆi+2ˆj+3ˆk and →b=2ˆi+3ˆj+ˆk , find a unit vector in the direction of (2→a+→b).
View SolutionIf →a=ˆi+ˆj+2ˆk and →b=3ˆi+2ˆj−ˆk, find the value of(→a+3→b). (2→a−→b).
View SolutionFind the unit vectors perpendicular to both →a and →b when
(i) →a=3ˆi+ˆj−2ˆk and →b=2ˆi+3ˆj−ˆk
(ii) →a=ˆi−2ˆj+3ˆk and →b=ˆi+2ˆj−ˆk
(iii) →a=ˆi+3ˆj−2ˆk and →b=−ˆi+3ˆk
(iv) →a=4ˆi+2ˆj−ˆk and →b=ˆi+4ˆj−ˆk
View SolutionFind the scalar and vector components of →a in the direction of →b where
→a=3ˆi+→j+3ˆkand→b=ˆi−ˆj−ˆk
View SolutionLet →a=ˆi+ˆj+ˆk,→b=2ˆi+3ˆj
→c=3ˆi+5ˆj−2ˆk, →d=−ˆj+ˆk
(i) Find →b−→a.
(ii) Find the unit vector along →b−→a.
(iii) Prove that →b−→a and →d−→c are parallel vectors.
View SolutionFor given vectors →a=2ˆi−ˆj+2ˆk and →b=−ˆi+ˆj−ˆk, find the unit vector in the direction of the vector →a+→b.
View SolutionIf →a=ˆi+ˆj+ˆk, →b=2ˆi−ˆj+3ˆk and →c=ˆi−2ˆj+ˆk, find a unit vector parallel to the vector 2→a−→b+3→c
View Solution
